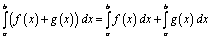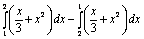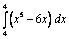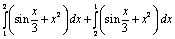Тема: Решение упражнений по теме «Интеграл. Формула Ньютона - Лейбница»

.Проверка домашнего задания

Устные упражнения:

1. Найдите какую — либо первообразную функции: а) f(x) = х³+4; б)g(x) = х²+х; в)q(x)=х¹⁰ — х^-3; г)t(x)= х^2/3 +1; е)d(x)=2х⁵-3х²; д)f(x)=3х³+2х-1; з)f(x)=3cosx-4sinx.

2. Найдите множество всех первообразных функции: а) f(x) = х15-х^-6; б)g(x) =1/х⁵+2,7;

в)q(x)=х^-2 —1/ х⁴.

3. Докажите двумя способами, что функция F является первообразной функции f, если: а) F(x) = х³/3- x⁵/5; f(x) = х2- х⁴; б)F(x)=х⁷/7 +х¹⁶/6; f(x)= х⁶ +х¹⁵ (Использовать в одном способе определение первообразной, в другом — теорему о нахождении первообразной суммы функций).

4. Известно, что скорость изменения функции F находится по формуле v (x)= x²+x. Задайте формулой функцию F, если F(0)=0.

5. Скорость изменения функции G подчиняется закону v(x)=x³-x². Найдите функцию G, если известно, что ее график проходит через точку М(0;3).

6. Первообразная функции f имеет вид F(x)= х³+15. Найдите какую- либо первообразную функции: а)3f; б)14f; в)-7,5f.

7. Найдите одну из первообразных для функции: а) f(x)=7x⁶; б)g(x)=-9х³; в)m(x)=1,8х²; г)d(x)=5х^-2; д)w(x)=х/3.

Пользуясь геометрическим смыслом определенного интеграла, вычислите:

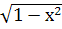; =у; 1- = ; + =1 – уравнение окружности с центром в начале координат и радиусом, равным 1.; =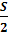

Ответ:

№ 6.33(б)

Пользуясь геометрическим смыслом определенного интеграла, вычислите: dх;

Площадь прямоугольника АКСД равна 3

Площадь треугольника ВКС равна ;

Тогда = 21- 9 =12

Ответ:

Для того, чтобы применять формулу Ньютона-Лейбница, нужно знать табличные значения неопределённых интегралов. Повторим таблицу первообразных:

(x )

+ C (n )

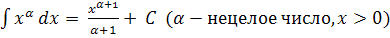
(x )

(x )

=

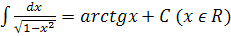
План:

1. Теорема Ньютона-Лейбница.

2. Вычисление определённого интеграла по формуле Ньютона-Лейбница.

3.Вычисление площади криволинейной трапеции, ограниченной линиями у=0, х=а, х=в, у=f(х), причем функция у=f(х) на интервале интегрирования принимает положительные и отрицательные значения.

4. Вычисление площади фигуры:

а) ограниченной линиями, у=f(х), х=а, х=в;

б) ограниченной линиями у= у= .

у=f(х), у= у= – функции непрерывные на области интегрирования.

Пусть функция f(x)непрерывная на отрезке и пусть F(х) есть какая-либо её первообразная. Тогда справедливо равенство Это равенство называют формулой Ньютона-Лейбница.

2.Объяснение вычисления определённого интеграла по формуле Ньютона-Лейбница

 

  Домашнее задание: Краткое сообщение «Исторические сведения о великих ученых И.Ньютоне и Г. Лейбнице»,,выучить конспект, законспектировать, решить:

Вариант №1	Вариант №2
Найдите неопределенный интеграл:
1) ; 2) ; 3) .	1) ; 2) ; 3) .

 

Основные свойства определенного интеграла
Карточка №1			Карточка №2
Найдите определенный интеграл
1)	2)		1)	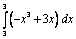2)
3)			3)
4)	5)		4)	5)
6)			6)
Карточка №3			Карточка №4
Найдите определенный интеграл
1)			1)
2)			2)
3)			3)
4)			4)
5)			5)
6)			6)