Методика выявления влияния фактора на дисперсионную модель в однофакторным случае

При наличии одного фактора, влияние которого исследуется, дисперсионный анализ именуется однофакторным и распадается на две разновидности:

- анализ несвязанных (различных) выборок. Например, одна группа респондентов решает задачу в условиях тишины, вторая, находясь в шумной комнате. (В этом случае, к слову, нулевая гипотеза звучала бы так: «среднее время решения задач такого-то типа будет одинаково в тишине и в условиях шумного помещения, то есть не зависит от фактора шума».);

- анализ связанных выборок, например, двух замеров, проведенных на одной и той же группе респондентов в разных условиях. Тот же пример: в первый раз задача решалась в тишине, второй - сходная задача - в условиях шумовых помех. (На практике к подобным опытам следует подходить с осторожностью, поскольку в действие может вступить неучтенный фактор «научаемость», влияние которого исследователь рискует приписать изменению условий, а именно, - шуму.)

В дисперсионном анализе анализируются не сами суммы квадратов отклонений, а так называемые средние квадраты, являющиеся несмещенными оценками соответствующих дисперсий, которые получаются делением сумм квадратов отклонений на соответствующее число степеней свободы.

Число степеней свободы определяется как общее число наблюдений минус число связывающих их уравнений.

 

Методика выявления влияния фактора на дисперсионную модель в однофакторным случае

В случае если исследуется одновременное воздействие двух или более факторов, мы имеем дело с многофакторным дисперсионным анализом, который также можно подразделить по типу выборки.

Если же воздействию факторов подвержено несколько переменных, - речь идет о многомерном анализе.

Многофакторный дисперсионный анализ

Следует сразу же отметить, что принципиальной разницы между многофакторным и однофакторным дисперсионным анализом нет. Многофакторный анализ не меняет общую логику дисперсионного анализа, а лишь несколько усложняет ее, поскольку, кроме учета влияния на зависимую переменную каждого из факторов по отдельности, следует оценивать и их совместное действие. Таким образом, то новое, что вносит в анализ данных многофакторный дисперсионный анализ, касается в основном возможности оценить межфакторное взаимодействие. Тем не менее, по-прежнему остается возможность оценивать влияние каждого фактора в отдельности. В этом смысле процедура многофакторного дисперсионного анализа несомненно более экономична, поскольку всего за один запуск решает сразу две задачи: оценивается влияние каждого из факторов и их взаимодействие.

Проверка нулевых гипотез H_A, H_B, H_AB об отсутствии влияния на рассматриваемую переменную факторов А, B и их взаимодействия AB осуществляется сравнением отношений,, (для модели I с фиксированными уровнями факторов) или отношений,, (для случайной модели II) с соответствующими табличными значениями F - критерия Фишера - Снедекора. Для смешанной модели III проверка гипотез относительно факторов с фиксированными уровнями производится также как и в модели II, а факторов со случайными уровнями - как в модели I.

Если n=1, т.е. при одном наблюдении в ячейке, то не все нулевые гипотезы могут быть проверены так как выпадает компонента Q₃ из общей суммы квадратов отклонений, а с ней и средний квадрат, так как в этом случае не может быть речи о взаимодействии факторов.

С точки зрения техники вычислений для нахождения сумм квадратов Q₁, Q₂, Q₃, Q₄, Q целесообразнее использовать формулы:

Q₃ = Q - Q₁ - Q₂ - Q₄.

Отклонение от основных предпосылок дисперсионного анализа -- нормальности распределения исследуемой переменной и равенства дисперсий в ячейках -- не сказывается существенно на результатах дисперсионного анализа при равном числе наблюдений в ячейках, но может быть очень чувствительно при неравном их числе. Кроме того, при неравном числе наблюдений в ячейках резко возрастает сложность аппарата дисперсионного анализа. Поэтому рекомендуется планировать схему с равным числом наблюдений в ячейках, а если встречаются недостающие данные, то возмещать их средними значениями других наблюдений в ячейках. При этом, однако, искусственно введенные недостающие данные не следует учитывать при подсчете числа степеней свободы

 

Основы регрессионного анализа. Регрессионная модель поведения системы. Метод наименьших квадратов как основной инструмент статистической обработки результатов группы экспериментов.

Регрессионный анализ — метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной). Регрессионная модель есть функция независимой переменной и параметров с добавленной случайной переменной. Параметры модели настраиваются таким образом, что модель наилучшим образом приближает данные. Критерием качества приближения (целевой функцией) обычно является среднеквадратичная ошибка: сумма квадратов разности значений модели и зависимой переменной для всех значений независимой переменной в качестве аргумента. Регрессионный анализ — раздел математической статистики и машинного обучения. Предполагается, что зависимая переменная есть сумма значений некоторой модели и случайной величины. Относительно характера распределения этой величины делаются предположения, называемые гипотезой порождения данных. Для подтверждения или опровержения этой гипотезы выполняются статистические тесты, называемые анализом остатков. При этом предполагается, что независимая переменная не содержит ошибок. Регрессионный анализ используется для прогноза, анализа временных рядов, тестирования гипотез и выявления скрытых взаимосвязей в данных.

Регрессия — зависимость математического ожидания (например, среднего значения) случайной величины от одной или нескольких других случайных величин (свободных переменных), то есть E (y /x)= f(x).

Регрессионным анализом называется поиск такой функции, которая описывает эту зависимость. Регрессия может быть представлена в виде суммы неслучайной и случайной составляющих.

Где F — функция регрессионной зависимости, а v — аддитивная случайная величина с нулевым матожиданием. Предположение о характере распределения этой величины называется гипотезой порождения данных. Обычно предполагается, что величина v имеет гауссово распределение с нулевым средним и дисперсией/

Задача нахождения регрессионной модели нескольких свободных переменных ставится следующим образом.

Задана выборка — множество значений свободных переменных и множество соответствующих им значений зависимой переменной. Эти множества обозначаются как, множество исходных данных. Задана регрессионная модель — параметрическое семейство функций f(w.x) зависящая от параметров w € R и свободных переменных x. Требуется найти наиболее

вероятные параметры w: 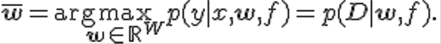Функция вероятности зависит от гипотезы порождения данных и задается Байесовским выводом или методом наибольшего правдоподобия.

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, Используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических минимальна

Метод наименьших квадратов — метод нахождения оптимальных параметров линейной регрессии, таких, что сумма квадратов ошибок (регрессионных остатков) минимальна. Метод заключается в минимизации евклидова расстояния между двумя векторами — вектором восстановленных значений зависимой | Aw-y | переменной и вектором фактических значений зависимой переменной.

Постановка задачи

Задача метода наименьших квадратов состоит в выборе вектора w, минимизирующего ошибку S=| Aw-y | ^2. Эта ошибка есть расстояние от вектора Y до вектора Aw. Вектор Aw лежит в простанстве столбцов матрицы A, так как Aw есть линейная комбинация столбцов этой матрицы с коэффициентами W1,….,Wn. Отыскание решения w по методу наименьших квадратов эквивалентно задаче отыскания такой точки P=Aw, которая лежит ближе всего к Y и находится при этом в пространстве столбцов матрицы A. Таким образом, вектор P должен быть проекцией Y на пространство столбцов и вектор невязки Aw-y должен быть ортогонален этому пространству. Ортогональность состоит в том, что каждый вектор в пространстве столбцов есть линейная комбинация столбцов с некоторыми коэффициентами v1,….,vn, то есть это вектор Av. Для всех v в пространстве Av, эти векторы должны быть перпендикулярны невязке Aw-y:  Так как это равенство должно быть справедливо для произвольного вектора, то  Решение по методу наименьших квадратов несовместной системы , состоящей из уравнений M с неизвестными N, есть уравнение  которое называется нормальным уравнением. Если столбцы матрицы A линейно независимы, то матрица A^T A обратима и единственное решение 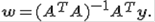 Проекция вектора Y на пространство столбцов матрицы имеет вид

Матрица называется матрицей проектирования вектора Y на пространство столбцов матрицы A. Эта матрица имеет два основных свойства: она идемпотентна, P^2=P, и симметрична, P^T=P. Обратное также верно: матрица, обладающая этими двумя свойствами есть матрица проектирования на свое пространство столбцов.

Основы регрессионного анализа. Выбор гипотетического вида регрессионной модели. Полиноминальная регрессия на отрезке, на кубе. Линейный и нелинейный регрессионный анализ. Линеаризация нелинейных моделей.

Основная цель регрессионного анализа состоит в определении аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимается за постоянные и средние значения.

Задачи регрессионного анализа: а) Установление формы зависимости. Относительно характера и формы зависимости между явлениями, различают положительную линейную и нелинейную и отрицательную линейную и нелинейную регрессию. б) Определение функции регрессии в виде математического уравнения того или иного типа и установление влияния объясняющих переменных на зависимую переменную. в) Оценка неизвестных значений зависимой переменной. С помощью функции регрессии можно воспроизвести значения зависимой переменной внутри интервала заданных значений объясняющих переменных (т. е. решить задачу интерполяции) или оценить течение процесса вне заданного интервала (т. е. решить задачу экстраполяции). Результат представляет собой оценку значения зависимой переменной.

Если в результате анализа пришли к выводу, что в регрессионной модели функция нелинейная, то обычно поступают так:

• подбирают такие преобразования анализируемых переменных , которые позволили бы представить искомую зависимость в виде линейного соотношения между новыми переменными:

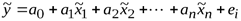, , …, − преобразования, , где

− это процедура линеаризации модели.

• при невозможности линеаризации модели исследуют регрессионную зависимость (нелинейную). Это значительно сложнее.

Различают два класса нелинейных регрессий:

• регрессии, нелинейные относительно включенных в анализ объясняющих переменных (факторов), но линейные по оцениваемым параметрам;
• регрессии, нелинейные по оцениваемым параметрам.

К первому классу относятся следующие функции:

• полиномы разных степеней − ,

, и т.д.

• гипербола − .

Ко второму классу относятся функции:

• степенная − ;
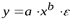• показательная − ;
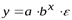• экспоненциальная − .

Нелинейная регрессия по включенным переменным представляет сложности в оценке параметров. Она определяется методом наименьших квадратов, ибо эти функции линейны по параметрам.

Если в результате предварительного анализа определяют вид нелинейной зависимости результативного показателя у от объясняющих переменных , то стараются линеаризовать уравнение, т.е. преобразовать нелинейную зависимость в линейную. Для оценки параметров нелинейных моделей используют два подхода.

Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую нелинейную зависимость представляют в виде линейной между преобразованными переменными.

Второй подход, основанный на применении методов нелинейной оптимизации, применяется в том случае, когда подобрать соответствующее преобразование не удается. Рассмотрим такие методы линеаризации нелинейных моделей, как замена переменных; логарифмирование обеих частей уравнения и комбинированные методы.

Таким образом, полином любого порядка сводится к линейной модели регрессии, для которой нами уже рассматривались методы оценивания параметров и проверки гипотез.

Полиномиальная регрессия означает приближение данных (xi, yi) полиномом k-й степени А(х)=а+bх+сх2+dх3+...+hxk (рис. 15.14). При k=1 полином является прямой линией, при k=2 — параболой, при k=3 — кубической параболой и т. д. Как правило, на практике применяются k<5.

Для построения регрессии полиномом k-й степени необходимо наличие по крайней мере (k+1) точек данных

Задача определения функциональной зависимости, наилучшим образом описывающей ЭД, связана с преодолением ряда принципиальных трудностей. В общем случае для стандартизованных данных функциональную зависимость показателя от параметров можно представить в виде

y = f (u₁, u₂,...u_p) + ε

где f – заранее не известная функция, подлежащая определению; ε - ошибка аппроксимации ЭД.

Указанное уравнение принято называть выборочным уравнением регрессии y на u. Это уравнение характеризует зависимость между вариацией показателя и вариациями факторов. А мера корреляции измеряет долю вариации показателя, которая связана с вариацией факторов. Иначе говоря, корреляцию показателя и факторов нельзя трактовать как связь их уровней, а регрессионный анализ не объясняет роли факторов в создании показателя.

Еще одна особенность касается оценки степени влияния каждого фактора на показатель. Регрессионное уравнение не обеспечивает оценку раздельного влияния каждого фактора на показатель, такая оценка возможна лишь в случае, когда все другие факторы не связаны с изучаемым. Если изучаемый фактор связан с другими, влияющими на показатель, то будет получена смешанная характеристика влияния фактора. Эта характеристика содержит как непосредственное влияние фактора, так и опосредованное влияние, оказанное через связь с другими факторами и их влиянием на показатель.

В регрессионное уравнение не рекомендуется включать факторы, слабо связанные с показателем, но тесно связанные с другими факторами. Не включают в уравнение и факторы, функционально связанные друг с другом (для них коэффициент корреляции равен 1). Включение таких факторов приводит к вырождению системы уравнений для оценок коэффициентов регрессии и к неопределенности решения.

Функция f должна подбираться так, чтобы ошибка ε в некотором смысле была минимальна. Существует бесконечное множество функций, описывающих ЭД абсолютно точно (ε = 0), т.е. таких функций, которые для всех значений параметров u_{j ,2} , u_{j ,3} , …, u_j,т принимают в точности соответствующие значения показателя y_i, i =1, 2, …, п. Вместе с тем, для всех других значений параметров, отсутствующих в результатах наблюдений, значения показателя могут принимать любые значения. Понятно, что такие функции не соответствуют действительной связи между параметрами и показателем.

В целях выбора функциональной связи заранее выдвигают гипотезу о том, к какому классу может принадлежать функция f, а затем подбирают "лучшую" функцию в этом классе. Выбранный класс функций должен обладать некоторой "гладкостью", т.е. "небольшие" изменения значений аргументов должны вызывать "небольшие" изменения значений функции (ЭД содержат некоторые ошибки измерений, а само поведение объекта подвержено влиянию помех, маскирующих истинную связь между параметрами и показателем).

Простым, удобным для практического применения и отвечающим указанному условию является класс полиномиальных функций

Для такого класса задача выбора функции сводится к задаче выбора значений коэффициентов a ₀ , a_j, a_jk, …, a_jj, …. Однако универсальность полиномиального представления обеспечивается только при возможности неограниченного увеличения степени полинома, что не всегда допустимо на практике, поэтому приходится применять и другие виды функций.

 

15. Методика однофакторного линейного РА с использованием матричной алгебры. Матрица факторов (модели). Информационная Х^Т Х (Фишера) и дисперсионные матрицы. Определение коэффициентов регрессионной модели. Сведение РМ к модели системы линейных уравнений.

Матрица, столбцы которой состоят из нагрузок данного фактора применительно ко всем переменным данной совокупности, а строки — из факторных нагрузок данной переменной, называется матрицей факторов, или факторной матрицей. Здесь также можно говорить о полной и редуцированной факторной матрице. Элементы полной факторной матрицы соответствуют полной единичной дисперсии каждой переменной из данной совокупности.

 Матрица ХТХ называется матрицей системы нормальных уравнений. Она обладает рядом важных свойств. Прежде всего заметим, что в этой матрице два элемента, расположенных симметрично относительно главной диагонали, равны между собой. В нашем случае ото нули. Такое свойство характерно для матриц систем нормальных уравнений МНК, так как векторы, входящие в скалярные произведения, коммутативны.

Решить систему нормальных уравнений это значит записать в явном виде элементы вектора В (b0 и b1). Воспользуется операцией умножения на обратную матрицу. (Эта операция превратит матрицу, стоящую перед матрицей неизвестных коэффициентов, в единичную). Чтобы равенство не нарушилось, и правую часть придется домножить на соответствующую матрицу.

(ХТХ)–1ХТХВ=(ХТХ)–1ХТY.

В этом равенстве участвуют три матрицы. Матрица системы нормальных уравнений ХТХ, которую называют прямой матрицей, (ХТХ)–1 – обратная матрица.

Продолжим вычисление для примера. Подставим известные матрицы в уравнение для вектора коэффициентов B==(ХТХ)–1ХТY.

Имеем

Матрица, определитель которой равен нулю, не имеет обратной. Такую матрицу называют особенной, вырожденной или сингулярной. Если же определитель матрицы не равен нулю, то матрица называется неособенной, невырожденной или несингулярной.

 

 

16. Методика многофакторного линейного РА с использованием матричной алгебры. Матрица факторов (модели). Информационная Х^Т Х (Фишера) и дисперсионные матрицы. Определение коэффициентов регрессионной модели. Сведение РМ к модели системы линейных уравнений.

Многофакторный линейный регрессионный анализ

Техника многофакторного регрессионного анализа в MSExcelпрактически не отличается от техники двухфакторного – используется тот же самый инструмент – Регрессия из пакета анализа. При этом предполагается, что в исходной таблице, описывающей случайные данные, каждый следующий столбец содержит выборку значений следующей по порядку случайной переменной; в соответствующем окошке указывается сплошная область значений влияющих переменных (факторов) многофакторной линейной модели.

Что касается сути самого анализа, в многофакторной регрессионной модели дополнительно учитываются и анализируются следующие характерные аспекты:

• коэффициент многофакторной детерминации (определение аналогично двухфакторной модели); с учетом сокращения степеней свободы, вызванным многофакторностью, применяется скорректированный коэффициент многофакторной детерминации , где - количество оцениваемых параметров;
• тест общей значимости качества регрессии; производится на основе статистики Фишера ( - распределение), для чего вычисляется значение 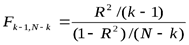, которое сравнивается с соответствующим критическим значением. Если вычисленное значение превосходит критическое при наперед заданном уровне значимости, то принимается гипотеза, что параметры регрессии не равны 0 и существенно отличается от 0.
• парциальные (частные) коэффициенты корреляции между факторами; парциальные коэффициенты корреляции вычисляются между каждым их влияющих факторов и зависимой переменной, очищенные от влияния остальных факторов. Так, например, для 3-факторной линейной регрессионной модели и , причем коэффициенты принимаются со знаками соответствующих параметров регрессии.

Специальным приемом в многофакторном регрессионном анализе явлений и процессов с наличием в них резких изменений (шоков) является использование грубых (шоковых) переменных. Присутствие шоков в модельных данных часто можно определить визуально (например, по виду диаграммы рассеяния). Шоковые переменные обычно задаются как бинарные, т.е. могут принимать только два различных значения – чаще всего 0 и 1. С их помощью моделируются резкие изменения в модели, вызванные психологическими, социальными, экономическими и т.п. стрессами. Дополнительная шоковая переменная D = (0,1) используется в технике регрессионного анализа наравне с другими переменными.

С использованием техники многофакторного регрессионного анализа проводится также статистический анализ распределенных лаговых моделей. Лаговые (с задержками) модели часто возникают в практике анализа случайных временных рядов; в моделях такого сорта предполагается, что на зависимую переменную оказывают влияние значения некоторой однородной объясняющей переменной, но в различные моменты (периоды) времени T. Общая форма такой модели выглядит следующим образом:

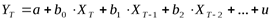
Приведение к стандартному виду такой «многофакторной» модели очевидно – «смещенные во времени» переменные рассматриваются как «независимые». Принципиальное отличие лаговой модели от «чистой» многофакторной – наличие сильных корреляций между «соседними» факторами.

Дисперсионная матрица - это квадратная таблица, характеризующая надежность, с которой определены неизвестные параметры. При этом диагональные элементы матрицы позволяют судить об ошибках в нахождении параметров, а недиагональные - о степени корреляционной связи между ними. В зависимости от дисперсионной матрицы оценок выбирается критерий оптимальности уточняющего плана. Обычно в качестве критерия используют А -, Д -, Е - критерии или их линейные или нелинейные комбинации.

+ все из 15 вопроса