Оценка точности НЛРМ производится по величине остаточной дисперсии, определяемой по формуле
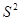 =
= 
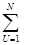 (b
(b  + b
+ b  Xu – Yu)
Xu – Yu)  , (7.15)
, (7.15)
где N – число опытов в таблице 1; b  , b
, b 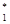 - коэффициенты регрессии, Xu, Yu – значения фактора и показателя в различных опытах.
- коэффициенты регрессии, Xu, Yu – значения фактора и показателя в различных опытах.
Оценка точности коэффициентов регрессии
И проверка гипотез об их значимости
Знание остаточной дисперсии позволяет определить дисперсии коэффициентов регрессии по формулам:
 {b
{b  } =
} = 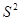 /{N – [ (
/{N – [ ( )
)  /
/  ]} (7.16)
]} (7.16)
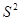 {b
{b 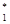 } =
} =  / {
/ {  - [ (
- [ ( )
)  / N]} (7.17)
/ N]} (7.17)
Ранее указывалось, что абсолютное значение коэффициента регрессии b 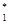 может быть близким нулю. В этом случае необходимо произвести проверку гипотезы о равенстве нулю данного КР.
может быть близким нулю. В этом случае необходимо произвести проверку гипотезы о равенстве нулю данного КР.
Математическая постановка и решение данной задачи записывается следующим образом:
1. Определяется нулевая гипотеза
Ho: b 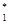 = 0 (7.18)
= 0 (7.18)
при альтернативной гипотезе
H  : b
: b  ¹ 0 (7.19)
¹ 0 (7.19)
2. Производится проверка гипотезы (7.18) с помощью t – распределения Стьюдента. Определяется расчетное значение t – критерия
t* = b 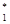 /
/  {b
{b  } (7.20)
} (7.20)
3. Значение (7.20) сравнивается с табличным значением 
 при
при
числе свободы n = N – 2 и доверительном уровне a (обычно 0.95).
При
| t*| > 
 (7.21)
(7.21)
гипотеза (7.18) отвергается и принимается гипотеза (7.19).
Аналогичным образом производится проверка значимости других КР. Отметим, что в случае принятия нулевой гипотезы соответствующий коэффициент регрессии приравнивается нулю (признается незначимым) и соответствующая степенная функция исключается из модели. Затем производится уточнение остальных (значимых) КР, остаточной дисперсии и дисперсий коэффициентов регрессии.
 2020-06-10
2020-06-10 167
167








