Задача 19 (демонстрационный вариант 2020 г.).
Задача 1
В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали,
по крайней мере, 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы № 1 в школу № 2,
а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Решение. а) Пусть в школе № 1 писали тест 2 учащихся, один из них набрал
1 балл, а второй набрал 19 баллов и перешёл в школу № 2. Тогда средний балл в школе № 1 уменьшился в 10 раз.
б) Пусть в школе № 2 писали тест  учащихся, средний балл равнялся
учащихся, средний балл равнялся 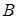 ,
,
а перешедший в неё учащийся набрал  баллов. Тогда получаем:
баллов. Тогда получаем:
 ;
;  .
.
Если  , то
, то  не делится на 10, а
не делится на 10, а  делится на 10. Но это невозможно, поскольку
делится на 10. Но это невозможно, поскольку  .
.
в) Пусть в школе № 1 средний балл равнялся  . Тогда получаем:
. Тогда получаем:
 ;
;  .
.
Заметим, что если  или
или 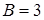 , то
, то  не делится на 10. Если
не делится на 10. Если 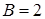 или
или  , то
, то 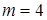 . В первом случае
. В первом случае  , а во втором
, а во втором  . Значит, ни один из этих случаев не возможен.
. Значит, ни один из этих случаев не возможен.
При  и
и  получаем
получаем  и
и  . Этот случай реализуется, например, если в школе № 1 писали тест 6 учащихся, 3 из них набрали
. Этот случай реализуется, например, если в школе № 1 писали тест 6 учащихся, 3 из них набрали
по 1 баллу, а 3 — по 3 балла, в школе № 2 писали тест 3 учащихся и каждый набрал по 5 баллов, а у перешедшего из одной школы в другую учащегося –
3 балла.
Ответ: а) да; б) нет; в) 5.
| Содержание критерия | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | 2 |
| Верно получен один из следующих результатов: – обоснованное решение пункта а; – обоснованное решение пункта б; – искомая оценка в пункте в; – пример в пункте в, обеспечивающий точность предыдущей оценки | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Задача 2
В последовательности  ,
,  , …,
, …, 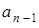 ,
,  , состоящей из целых чисел,
, состоящей из целых чисел,
 ,
, 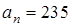 . Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
. Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
а) Приведите пример такой последовательности.
б) Может ли такая последовательность состоять из 1000 членов?
в) Из какого наименьшего числа членов может состоять такая последовательность?
Решение.
а) Например, последовательность 1, 2, 3, 0, 5,  , 7,
, 7,  , …, 233,
, …, 233,  , 235
, 235
удовлетворяет условию задачи (чередуются суммы чисел 3 и 5).
б) Поскольку 3, 5 и 25 — нечётные числа, любые два соседних члена последовательности имеют разную чётность. На нечётных местах должны стоять нечётные числа, а на чётных — чётные. Число 235 нечётное, поэтому оно не может стоять на чётном месте. Значит, последовательность не может состоять из 1000 членов.
в) Рассмотрим три члена последовательности: 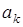 ,
,  ,
, 
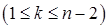 .
.
Поскольку 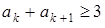 ,
,  , получаем:
, получаем:  .
.
В предыдущем пункте было показано, что последовательность должна состоять из нечётного числа членов. Пусть  , тогда
, тогда
 ;
; 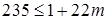 ,
,
откуда  . Значит, последовательность состоит не менее чем из 23 чисел.
. Значит, последовательность состоит не менее чем из 23 чисел.
Приведём пример последовательности, удовлетворяющей условию задачи, состоящей из 23 членов: 1, 2, 23,  , 45,
, 45,  , 67,
, 67,  , 89,
, 89,  , 111,
, 111,  ,
,  ,
,  , 155,
, 155,  , 175,
, 175,  , 195,
, 195,  , 215,
, 215,  , 235.
, 235.
Ответ: а) например, 1, 2, 3, 0, 5,  , 7,
, 7,  , …, 233,
, …, 233,  , 235; б) нет; в) 23.
, 235; б) нет; в) 23.
| Содержание критерия | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | 2 |
| Верно получен один из следующих результатов: — пример в п. а; — обоснованное решение п. б; — искомая оценка в п. в; — пример в п. в, обеспечивающий точность предыдущей оценки | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Задача 3
На доске написано 30 натуральных чисел (числа могут повторяться), каждое из которых либо зелёного, либо красного цвета. Каждое зелёное число кратно 3, а каждое красное число кратно 7. При этом все зелёные числа различны
и все красные различны (какое-то зелёное число может равняться какому-то красному числу).
а) Может ли сумма написанных чисел быть меньше  , если все числа на доске кратны 3?
, если все числа на доске кратны 3?
б) Может ли ровно одно число на доске быть красным, если сумма написанных чисел равна 1067?
в) Какое наименьшее количество красных чисел может быть на доске, если сумма написанных чисел равна 1067?
Решение.
а) Если на доске записано 29 зелёных чисел: 3, 6, …, 87 — и одно красное
число 21, то их сумма меньше 1395.
б) Пусть на доске ровно одно красное число. Тогда зелёных чисел 29,
а их сумма не меньше, чем сумма 29 наименьших чисел, делящихся на 3:
 .
.
Это противоречит тому, что сумма написанных чисел равна 1067.
в) Пусть на доске написано  красных чисел и
красных чисел и  зелёных чисел. Тогда сумма красных чисел не меньше
зелёных чисел. Тогда сумма красных чисел не меньше  ,
,
а сумма зелёных чисел не меньше
 .
.
Таким образом,  ;
;  ,
,
откуда, учитывая, что  — целое, получаем
— целое, получаем  .
.
Приведём пример 6 красных чисел и 24 зелёных чисел, сумма которых
равна 1067: 7, 14, 21, 28, 35, 56, 3, 6, …, 66, 69, 78.
Ответ: а) да; б) нет; в) 6.
| Содержание критерия | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | 2 |
| Верно получен один из следующих результатов: — обоснованное решение пункта а; — обоснованное решение пункта б; — искомая оценка в пункте в; — пример в пункте в, обеспечивающий точность предыдущей оценки | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Пример 1.
В последовательности  ,
,  , …,
, …, 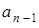 ,
,  , состоящей из целых чисел,
, состоящей из целых чисел,
 ,
, 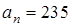 . Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
. Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
а) Приведите пример такой последовательности.
б) Может ли такая последовательность состоять из 1000 членов?
в) Из какого наименьшего числа членов может состоять такая последовательность?
Ответ: а) например, 1, 2, 3, 0, 5,  , 7,
, 7,  , …, 233,
, …, 233,  , 235; б) нет; в) 23.
, 235; б) нет; в) 23.

Комментарий.
В пункте а допущена ошибка – сумма первых двух чисел равна –25. При ответе на вопрос пункта б участник экзамена верно показал, что случай  невозможен.
невозможен.
Оценка эксперта: 1 балл.
Пример 2.
На столе лежит 40 карточек, часть из которых красного цвета, а остальные синего (есть хотя бы по одной карточке каждого цвета). На каждой карточке написано натуральное число. Все числа, написанные на синих карточках, различны. Любое число на красной карточке меньше любого числа на синей карточке. Среднее арифметическое всех чисел на карточках равно 14. Если утроить числа на синих карточках, то среднее арифметическое всех чисел станет равно 39.
а) Может ли на столе быть ровно 10 синих карточек?
б) Может ли на столе быть ровно 10 красных карточек?
в) Какое наибольшее количество синих карточек может быть на столе?
Ответ: а) да; б) нет; в) 26.

Комментарий.
В решении пункта а есть только описание чисел, написанных на синих карточках. Указания чисел, написанных на красных карточках, отсутствует. В решении пункта б допущена вычислительная ошибка. Решение пункта в отсутствует.
 2020-06-10
2020-06-10 162
162







