В упругом анизотропном теле каждый из компонентов напряжений может зависеть от всех составляющих деформаций:
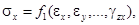
……………………………
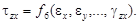
Ограничиваясь малыми деформациями, связь между напряжениями и деформациями можно принять линейной:
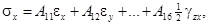
…………………………………………..
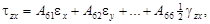
где А 11, А 12,…, А 66 – жесткости линейно-упругого состояния тела (упругие жесткости). Эти зависимости называются уравнениями обобщенного закона Гука в прямой форме. Прообразом является физический закон, обнаруженный Р. Гуком из опыта при одноосном напряженном состоянии тела.
Обратные соотношения имеют вид
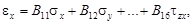
…………………………………………..
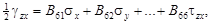
где B 11, В 12,…, B 66 – податливости линейно-упругого состояния тела (упругие податливости). Чем больше Аij, тем (при неизменности деформаций) бóльшими будут напряжения, т.е. тем жестче тело. Чем больше Вij, тем (при неизменности напряжений) бóльшими будут деформации, т.е. тем податливее тело.
Обобщенный закон Гука можно представить в матричной форме:
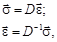
где 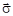 – вектор напряжений;
– вектор напряжений; 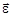 – вектор деформаций;
– вектор деформаций;
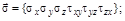
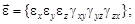
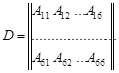
Матрица D называется матрицей упругих жесткостей (матрицей упругости). Обратная матрица D -1 по смыслу является матрицей упругих податливостей.
Поскольку упругому телу присущи обратимые процессы деформирования, то при использовании потенциальной функции напряжений можно обнаружить, что Аij = Аji. Следовательно, коэффициенты, расположенные симметрично относительно главной диагонали матрицы, попарно равны между собой. Тогда в анизотропном теле число упругих постоянных оказывается равным 21.
Предположим, что одна из координатных плоскостей, например, плоскость хОу, является плоскостью симметрии упругих свойств. Тогда следует заменить τ xz и τ yz на (–τ xz) и (–τ yz) соответственно, а γ xz и γ yz – на (–γ xz) и (–γ yz). При неизменности физических соотношений ряд коэффициентов обращается в нуль:
A 15 = A 16 = A 25 = A 26 = A 35 = A 36 = A 45 = A 46 = 0.
Так, число упругих постоянных при наличии только одной плоскости симметрии сокращается до 13.
В случае, если через каждую точку тела проходят три ортогональные плоскости симметрии упругих свойств (ортотропное тело), число независимых постоянных снижается до 9 (А 14 = А 24 = А 34 = А56= 0).
Примерами ортотропных материалов служат дерево, фанера, железобетон, армированные пластики, холодный прокат черных металлов.
В случае полной симметрии (изотропное тело), когда любая плоскость есть плоскость упругой симметрии, имеем следующие физические уравнения:
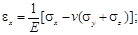
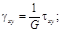
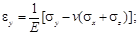
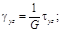
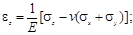
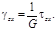
Упругие постоянные E, v и G взаимосвязаны. Это можно показать на примере вычисления деформации сдвига
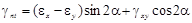
при совмещении осей x и y с главными осями 1 и 2:
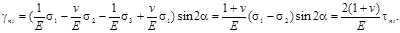
Имея в виду, что 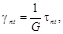 получаем
получаем
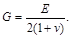
Следовательно, изотропное тело имеет две упругие постоянные, в качестве которых можно принять, например, модуль продольной упругости Е и коэффициент Пуассона v. Величина G называется модулем сдвига.
Запишем выражения для напряжений:
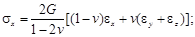
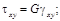
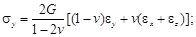
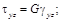
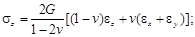
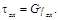
С учетом этих зависимостей вычислим удельную потенциальную энергию деформаций путем интегрирования
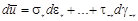
в пределах от 0 до εx,… при 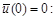
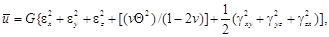
где:
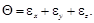
Выразив деформации через напряжения, получим
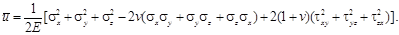
По физическому смыслу упомянутое выше интегрирование сводится к вычислению площадей треугольников на линейном участке диаграммы "напряжение − деформация", ограниченном деформациями ε x,…,γ zx соответственно:
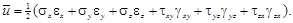
Следовательно, удельная потенциальная энергия деформации, накапливае-мая в упругом теле, равна полусумме произведений компонентов напряжений на соответствующие им компоненты деформации. Этот факт тесно связан с энергетической теоремой Клапейрона для линейно деформирующегося тела, в связи с чем соответствующую зависимость называют формулой Клапейрона.
Введем величины 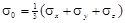 и
и 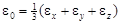 и предста-вим рассматриваемую энергию в виде двух составляющих.
и предста-вим рассматриваемую энергию в виде двух составляющих.
Удельная потенциальная энергия изменения объема равна
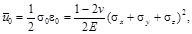
или
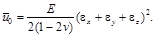
Удельная потенциальная энергия изменения формы равна
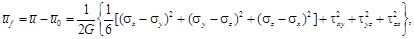
или
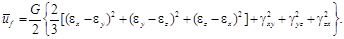
 2020-07-12
2020-07-12 133
133








