Синхронизация процессов – приведение двух или нескольких процессов к такому их протеканию, когда определённые стадии разных процессов совершаются в определённом порядке, либо одновременно.
Фазовая автоподстройка частоты (ФАПЧ) — система автоматического регулирования, подстраивающая фазу управляемого генератора так, чтобы она была равна фазе опорного сигнала, либо отличалась на известную функцию от времени.
Алгоритм Витерби – алгоритм поиска наиболее подходящего списка состояний (называемого путём Витерби), который получает наиболее вероятную последовательность произошедших событий.
Модифицированные функции Бесселя — это функции Бесселя от чистого мнимого аргумента.

Это уравнение называется модифицированным уравнением Бесселя .
Дисперсия фазы – это мера неустойчивой синхронизации на выходе генератора, управляемого напряжением, вследствие шума на входе.
Условие задачи:
Витерби показал, что функция плотности вероятности выходной фазы контура ФАПЧ первого порядка, возмущенная белым гауссовым шумом, описывается следующим выражением.
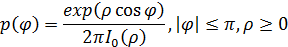
Покажите, что приведенное выше 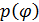 действительно является функцией плотности вероятности, и вычислите среднее и дисперсию
действительно является функцией плотности вероятности, и вычислите среднее и дисперсию 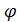 .
.
Дано:
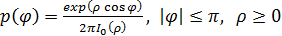 ,
,
где 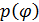 - функция плотности вероятности;
- функция плотности вероятности;
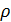 – нормированное отношение сигнал/шум
– нормированное отношение сигнал/шум
контура,
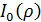 – модифицированная функция Бесселя
– модифицированная функция Бесселя
первого рода нулевого порядка, взятая в точке 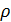 .
.
Найти:
1) Показать, что 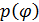 - является функцией плотности вероятности.
- является функцией плотности вероятности.
2) Среднее 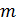 -?
-?
3) Дисперсию 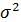 -?
-?
Решение:
1) Для решения данной задачи будем использовать основную формулу, приведенную ниже:
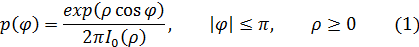
где 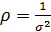 – нормированное отношение (на энергию единичного сигнала) сигнал/шум контура,
– нормированное отношение (на энергию единичного сигнала) сигнал/шум контура,
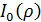 – модифицированная функция Бесселя первого рода нулевого порядка, взятая в точке
– модифицированная функция Бесселя первого рода нулевого порядка, взятая в точке 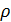 .
.
2) Для дальнейшего вычисления будем использовать измененную функцию Бесселя в интегральной форме, для нулевого порядка. Измененная функция Бесселя выражается следующей формулой:
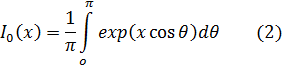
где 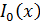 - модифицированная функция Бесселя первого рода нулевого порядка, взятая в точке
- модифицированная функция Бесселя первого рода нулевого порядка, взятая в точке 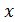 .
.
3) Для доказательства, что функция 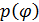 - является функцией плотности вероятности, рассмотрим ее основные свойства, которые приведены ниже:
- является функцией плотности вероятности, рассмотрим ее основные свойства, которые приведены ниже:
1. Плотность вероятностей принимает положительные значения:
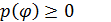
Это свойство следует из определения первой производной от функции распределения, которая в свою очередь является неубывающей функцией.
2. Условие нормирования случайной величины 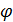 :
:
4) Докажем основные свойства функции плотности вероятности.
1. Плотность вероятностей принимает положительные значения, так как согласно условию задачи в формуле (1):  . Следует, и сама функция будет неотрицательной функцией,
. Следует, и сама функция будет неотрицательной функцией,  .
.
2. Условие нормирования случайной величины 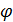 также выполняется:
также выполняется:
Интеграл  является единицей (единством), когда интегрирован в пределах
является единицей (единством), когда интегрирован в пределах  .
.
Выполняются оба основных свойства, поэтому функция 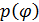 - является функцией плотности вероятности.
- является функцией плотности вероятности.
5) Значение 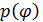 равно нулю в случае, если среднее
равно нулю в случае, если среднее 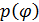 такжеравно нулю, что видно из формулы приведенной ниже:
такжеравно нулю, что видно из формулы приведенной ниже:
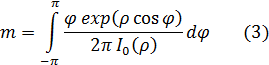
где 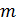 – среднее от функции
– среднее от функции 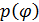 ;
;
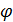 – скачок фазы.
– скачок фазы.
6)Используя формулу (3), определяем формулу для вычисления дисперсии сдедующим способом:
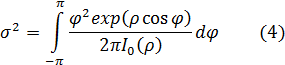
где 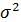 – дисперсия;
– дисперсия;
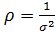 – нормированное отношение (на энергию единичного сигнала) сигнал/шум контура,
– нормированное отношение (на энергию единичного сигнала) сигнал/шум контура,
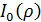 – модифицированная функция Бесселя первого рода нулевого порядка, взятая в точке
– модифицированная функция Бесселя первого рода нулевого порядка, взятая в точке 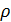 .
.
7) Преобразовывая формулу (2), получаем следующее выражение:

8) Объединяя выражения (4) и (5), находим конечную формулу для вычисления дисперсии:
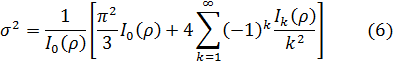
Ответ:
1) 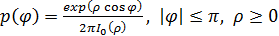 – действительно является функцией плотности вероятности.
– действительно является функцией плотности вероятности.
2) Среднее от 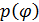 равно
равно 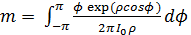 .
.
3) Дисперсия равна 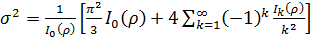 .
.
Заключение
Для решения задачи мы использовали алгоритм декодирования, основанный на принципе максимального правдоподобия, описываемый формулой Витерби.
Витерби определил, что для контура ФАПЧ первого порядка (т.е. контурный фильтр) — это просто цепь короткого замыкания, или, что эквивалентно, f(t) = d (t) функция плотности вероятности 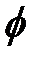 имеет следующий вид.
имеет следующий вид.
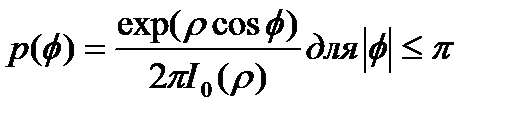
Здесь 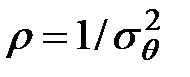 — нормированное (на энергию единичного сигнала) отношение сигнал/шум контура, а I 0(
— нормированное (на энергию единичного сигнала) отношение сигнал/шум контура, а I 0(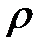 ) — модифицированная функция Бесселя первого рода нулевого порядка, взятая в точке
) — модифицированная функция Бесселя первого рода нулевого порядка, взятая в точке 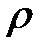 .
.
 2020-07-12
2020-07-12 150
150








