Неевклидова геометрия Римана имеет много общего с обычной геометрией Евклида. Так, например, здесь также справедливы теоремы о сравнительной длине сторон треугольника (каждая сторона меньше суммы двух других и больше их разности), о свойствах равнобедренного треугольника, о замечательных точках треугольника. Справедливы также и признаки равенства треугольников. Только наряду с "третьим признаком равенства треугольников" (два треугольника равны, если стороны одного соответственно равны сторонам другого) в неевклидовой геометрии Римана имеет место еще так называемый "четвертый признак равенства треугольников": два треугольника равны, если углы одного из них соответственно равны углам второго. Первый и второй признаки равенства треугольников доказываются так же, как и в случае евклидовой геометрии: с использованием "неевклидовых движений", роль которых играют повороты неевклидовой плоскости Римана вокруг точки и симметрии относительно прямой (см. Рис. 4).
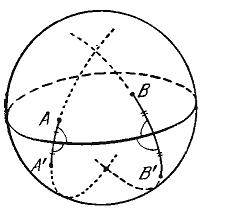
Рис. 4
Третий признак равенства треугольников также может быть доказан с помощью обычного приема ‒ с использованием теорем о равнобедренном треугольнике, вывод которых не составляет труда (см. Рис. 5). Наконец, четвертый признак равенства треугольников получается из третьего с помощью принципа двойственности.
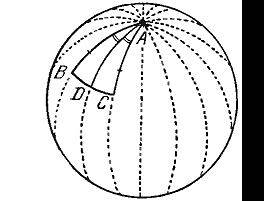
Рис. 5
Теоремы о точке пересечения биссектрис треугольника  и о точке пересечения перпендикуляров, восстановленных к сторонам треугольника в их серединах, доказываются в точности так же, как в геометрии Евклида. Первая из этих точек является центром вписанной в треугольник
и о точке пересечения перпендикуляров, восстановленных к сторонам треугольника в их серединах, доказываются в точности так же, как в геометрии Евклида. Первая из этих точек является центром вписанной в треугольник  окружности (см. Рис. 6, а), а вторая ‒ центром описанной окружности (см. Рис. 6, б).
окружности (см. Рис. 6, а), а вторая ‒ центром описанной окружности (см. Рис. 6, б).
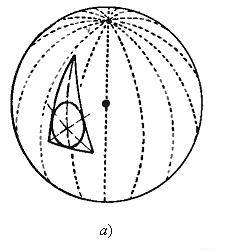
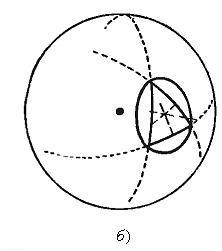
Рис. 6
До сих пор мы больше говорили о тех теоремах неевклидовой геометрии Римана, которые аналогичны известным теоремам евклидовой геометрии. Для того чтобы дать представление о различии этих двух геометрий, остановимся на вопросе о площади многоугольника в неевклидовой геометрии Римана. Вспомним прежде всего, что в этой геометрии сумма углов треугольника всегда больше  . Отсюда можно вывести, что сумма углов n -угольника в неевклидовой геометрии Римана всегда больше
. Отсюда можно вывести, что сумма углов n -угольника в неевклидовой геометрии Римана всегда больше 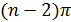 . В самом деле, каждый n -угольник можно разбить на
. В самом деле, каждый n -угольник можно разбить на 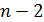 треугольников непересекающимися диагоналями, это относится как к неевклидовой геометрии Римана, так и к обычной геометрии Евклида. Случай
треугольников непересекающимися диагоналями, это относится как к неевклидовой геометрии Римана, так и к обычной геометрии Евклида. Случай 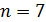 изображен на Рис. 7.
изображен на Рис. 7.
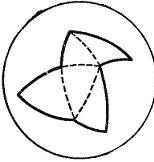
Рис. 7
При этом сумма углов n -угольника равна сумме всех углов всех 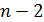 треугольников, отсюда и вытекает, что сумма углов n -угольника в неевклидовой геометрии Римана всегда больше
треугольников, отсюда и вытекает, что сумма углов n -угольника в неевклидовой геометрии Римана всегда больше 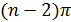 .
.
Задача измерения площадей состоит в том, чтобы сопоставить каждому многоугольнику 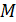 некоторое число
некоторое число 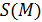 ‒ площадь этого многоугольника ‒ с соблюдением следующих требований:
‒ площадь этого многоугольника ‒ с соблюдением следующих требований:
a) положительность: для любого многоугольника 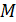 (содержащего внутренние точки)
(содержащего внутренние точки) 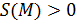 ;
;
b) инвариантность: если многоугольники  и
и 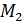 равны, то
равны, то 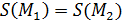 ;
;
c) аддитивность: если многоугольник 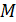 разбит на неперекрывающиеся части
разбит на неперекрывающиеся части  и
и 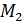 , то
, то 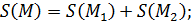
d) нормировка: для многоугольника 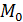 , признанного "единичным",
, признанного "единичным", 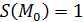 .
.
Такое аксиоматическое определение площади является осмысленным лишь в том случае, если действительно существует функция  , сопоставляющая каждому многоугольнику
, сопоставляющая каждому многоугольнику 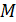 число
число 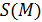 с указаными свойствами, и притом такая функция имеется лишь одна. В неевклидовой геометрии Римана также существует теорема о том, что условия
с указаными свойствами, и притом такая функция имеется лишь одна. В неевклидовой геометрии Римана также существует теорема о том, что условия 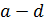 однозначно определяет
однозначно определяет 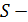 площадь. Впрочем, существование функции
площадь. Впрочем, существование функции  будет ясно из дальнейшего, так как мы укажем угловой избыток, удовлетворяющую условиям
будет ясно из дальнейшего, так как мы укажем угловой избыток, удовлетворяющую условиям 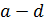 . Единственность же позволит утверждать, что указанная величина, угловой избыток как раз и является площадью, поскольку, кроме нее, не существует никакой другой функции, удовлетворяющей условиям
. Единственность же позволит утверждать, что указанная величина, угловой избыток как раз и является площадью, поскольку, кроме нее, не существует никакой другой функции, удовлетворяющей условиям 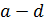 . Таким образом, единственность является важным элементом при построении теории площадей, и если мы опускаем здесь доказательство единственности, то не из-за его малой значимости, а лишь из-за нежелания перегружать статью.
. Таким образом, единственность является важным элементом при построении теории площадей, и если мы опускаем здесь доказательство единственности, то не из-за его малой значимости, а лишь из-за нежелания перегружать статью.
Очень просто указать число, удовлетворяющее наиболее важным условиям 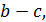 в качестве него можно взять угловой избыток в
в качестве него можно взять угловой избыток в 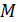 рассматриваемого n -угольника
рассматриваемого n -угольника 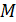 , то есть превышение суммы его углов над
, то есть превышение суммы его углов над 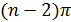 ;
;
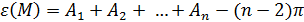
здесь 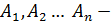 углы n -угольника, измеренные в радианной мере. В самом деле, поскольку равные многоугольники
углы n -угольника, измеренные в радианной мере. В самом деле, поскольку равные многоугольники  и
и 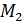 имеют одинаковые углы, то и избытки их, очевидно, равны:
имеют одинаковые углы, то и избытки их, очевидно, равны:
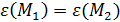 ;
;
таким образом, свойство инвариантности выполнено.
В евклидовой геометрии аддитивность углового избытка никак не может быть использована для построения теории площадей: она является просто следствием того обидного с точки зрения наших настоящих интересов обстоятельства, что угловой избыток каждого многоугольника равен в евклидовой геометрии нулю. Однако в неевклидовой геометрии Римана угловой избыток положителен, то есть удовлетворяет условию 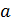 . Таким образом, для того чтобы получить величину, удовлетворяющую всем четырем условиям
. Таким образом, для того чтобы получить величину, удовлетворяющую всем четырем условиям 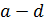 , надо лишь нормировать угловой избыток, умножив его на постоянный множитель пропорциональности
, надо лишь нормировать угловой избыток, умножив его на постоянный множитель пропорциональности 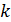 с тем, чтобы соблюдалось и условие
с тем, чтобы соблюдалось и условие 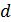 . При этом выбор числа
. При этом выбор числа 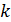 существенно зависит от выбора единицы измерения площадей.
существенно зависит от выбора единицы измерения площадей.
Выберем эту единицу так, чтобы треугольник с тремя прямыми углами имел площадь, равную его угловому избытку, то есть равную 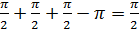 , при этом площадь всей сферы будет равна
, при этом площадь всей сферы будет равна 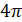 .
.
Таким образом, радиус сферы принимается здесь за 1, а площадь всей неевклидовой плоскости Римана равна 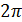 . При этом будем иметь
. При этом будем иметь 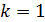 , то есть площадь каждого многоугольника будет равна его угловому избытку:
, то есть площадь каждого многоугольника будет равна его угловому избытку:
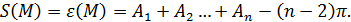
 2020-07-12
2020-07-12 330
330








