Из элементарной геометрии нам известна формула площади треугольника  через длины его сторон
через длины его сторон  , которая может быть представлена в следующем виде:
, которая может быть представлена в следующем виде:
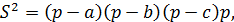
где 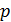 — полупериметр треугольника. Данная формула известна как формула Герона, названной так по имени Герона Александрийского, выдающегося древнегреческого математика, жившего в I в.н.э. Формула Герона выражает площадь треугольника через длины его сторон, а для многоугольников с большим количеством сторон формулы такого типа не существует, так как площадь многоугольника может меняться при его изгибании с сохранением длин сторон. Площадь четырёхугольника, вообще говоря, не определяется через длины его сторон. Однако, это справедливо в некоторых частных случаях, например, когда четырёхугольник является вписанным, либо когда он представляет собой трапецию. В первом случае нам известна теорема Брахмагупты, а именно, площадь
— полупериметр треугольника. Данная формула известна как формула Герона, названной так по имени Герона Александрийского, выдающегося древнегреческого математика, жившего в I в.н.э. Формула Герона выражает площадь треугольника через длины его сторон, а для многоугольников с большим количеством сторон формулы такого типа не существует, так как площадь многоугольника может меняться при его изгибании с сохранением длин сторон. Площадь четырёхугольника, вообще говоря, не определяется через длины его сторон. Однако, это справедливо в некоторых частных случаях, например, когда четырёхугольник является вписанным, либо когда он представляет собой трапецию. В первом случае нам известна теорема Брахмагупты, а именно, площадь  вписанного в окружность четырёхугольника со сторонами
вписанного в окружность четырёхугольника со сторонами 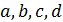 и полупериметром
и полупериметром  — равна:
— равна:
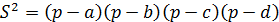 .
.
Формула Брахмагупты является обобщением формулы Герона. Формулировку и доказательство данной теоремы можно найти в книге ([2], с. 90). Немецкий математик Карл Бретшнайдер в 1842 году нашел площадь произвольного евклидова четырехугольника. Классическая теорема Бретшнайдера [3] утверждает, что площадь  евклидова четырехугольника со сторонами
евклидова четырехугольника со сторонами 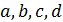 и противолежащими углами
и противолежащими углами 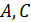 находится по формуле:
находится по формуле:
 ,
,
где 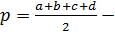 полупериметр четырехугольника ([2], с. 89).
полупериметр четырехугольника ([2], с. 89).
Определение 3[4]. Выпуклый четырёхугольник ABCD называется трапецией, если для его внутренних углов справедливо соотношение:
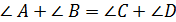 .
.
В этом случае стороны 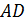 и
и  называются основаниями трапеции
называются основаниями трапеции 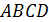 , а
, а 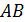 и
и  ‒ её боковыми сторонами,
‒ её боковыми сторонами, 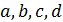 ‒ соответствующие длины сторон трапеции,
‒ соответствующие длины сторон трапеции, 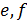 ‒ длины диагоналей
‒ длины диагоналей 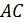 и
и 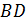 . Всюду в дальнейшем будем предполагать, что
. Всюду в дальнейшем будем предполагать, что 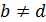 . Сформулируем основную теорему.
. Сформулируем основную теорему.
Теорема 3[4]. Площадь  сферической трапеции
сферической трапеции 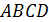 со сторонами
со сторонами 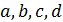 находится из соотношения:
находится из соотношения:
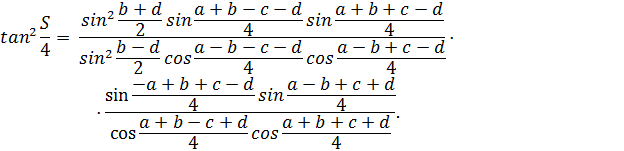
Замечание 1. 1. Площадь 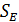 евклидовой трапеции со сторонами
евклидовой трапеции со сторонами 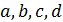 вычисляется по формуле:
вычисляется по формуле:
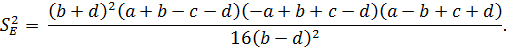
Отметим, что 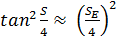 при достаточно малых величин
при достаточно малых величин 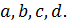
Теорема 4[4]. Площадь  сферического четырехугольника со сторонами
сферического четырехугольника со сторонами 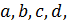 углами
углами 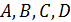 и полупериметром
и полупериметром 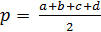 находится по формуле:
находится по формуле:
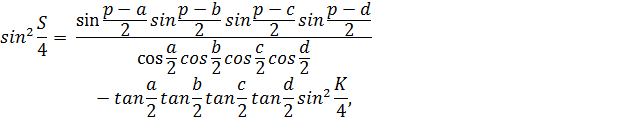
где 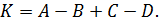
Следствие 2.1. Площадь  вписанного сферического четырехугольника со сторонами
вписанного сферического четырехугольника со сторонами 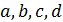 находится по формуле:
находится по формуле:

где 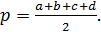
Следствие 2.2. Если сферический четырехугольник со сторонами 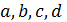 вписан в одну окружность и описан около другой, то его площадь
вписан в одну окружность и описан около другой, то его площадь  находится по формуле:
находится по формуле:
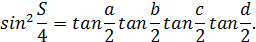
Следствие 2.3. Сферический четырехугольник со сторонами 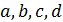 имеет максимальную площадь
имеет максимальную площадь  тогда и только тогда, когда он вписан в окружность.
тогда и только тогда, когда он вписан в окружность.
Теорема 5[4]. Площадь  гиперболического четырехугольника со сторонами
гиперболического четырехугольника со сторонами 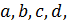 углами
углами 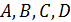 находится по формуле:
находится по формуле:
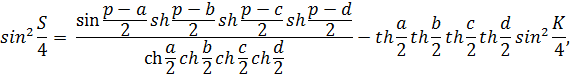
где 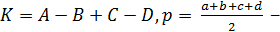 полупериметр.
полупериметр.
Следствие 3.1. Площадь  вписанного гиперболического четырехугольника со сторонами
вписанного гиперболического четырехугольника со сторонами 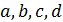 находится по формуле:
находится по формуле:
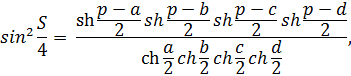
где 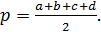
Следующее следствие выражает площадь описанного четырехугольника через стороны и четырехугольника со сторонами 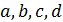 .
.
Следствие 3.2. Площадь  описанного гиперболического четырехугольника со сторонами
описанного гиперболического четырехугольника со сторонами 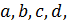 углами
углами 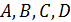 находится по формуле:
находится по формуле:
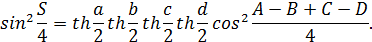
Следствие 3.3. Если гиперболический четырёхугольник со сторонами 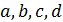 вписан в одну окружность и описан около другой, то его площадь S находится по формуле:
вписан в одну окружность и описан около другой, то его площадь S находится по формуле:
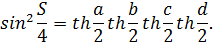
Следствие 3.4. Гиперболический четырёхугольник со сторонами 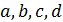 имеет максимальную площадь
имеет максимальную площадь  тогда и только тогда, когда он вписан в окружность, орицикл или в одну ветвь эквидистанты.
тогда и только тогда, когда он вписан в окружность, орицикл или в одну ветвь эквидистанты.
Заключение
В данной курсовой работе были изучены основные формулы площади неевклидовых многоугольников, где и как они используются. Основным направлением этого изучения являлась сферическая, гиперболическая геометрии.
Изучая теорию неевклидовой геометрии, я установила, что элементы некоторых фигур: углы, прямые, отрезки, многоугольники рассматриваются иначе, чем эти же фигуры на плоскости или в пространстве в евклидовой геометрии. Я узнала, что в геометрии сферы существует фигура, у которой менее трёх вершин – двуугольник. По-разному трактуются и знакомые нам теоремы. Применяются другие формулы для вычисления площади фигур.
Так как тема неевклидовой геометрии очень объемна, в работе была представлена лишь основная часть всех возможный понятий, формул, теорем, следствий и манипуляций. Изучение и описание которых заняло бы несравнимо большее время, чем дано одной человеческой жизни.
Список литературы
[1] Соколова, Д. Ю. О площади трапеции на плоскости Лобачевского / Д. Ю. Соколова // Сиб. электрон, матем. изв. - 2012. - Т. 9. - С. 256- 260.
[2] Понарин, Я. П. Элементарная геометрия. Т.1. Планиметрия / Я. П. Понарин. - М.: МЦНМО. 2004. - С. 312.
[3] Bretschneider, C. A. Untersuchung der trigonometrischen Relationen des geradlinigen Viereckes / C. A. Bretschneider // Arch. Math. - 1842. - Bd. 2. - S. 225-261.
[4] Байгонакова, Г. А. Аналитические методы в теории объемов многогранников в неевклидовой геометрии / Г. А. Байгонакова // Автореферат. -2013. -Т. - С. 10-16.
[5] Байгонакова, Г. А. Площадь трапеции в сферической геометрии / Г. А. Байгонакова, Д. Ю. Соколова // Материалы школы конференции по геометрическому анализу (Горно-Алтайск, И - 19 августа, 2012 г.). - Горно-Алтайск: РИО ГАГУ, 2012. - С. 12-13.
[6] Винберг, Э. Б. Геометрия 2. Современные проблемы математики / Э. Б. Винберг - М.: ВИНИТИ (Итоги науки и техники), 1988. Т. 29. - С. 1-146.
 2020-07-12
2020-07-12 165
165







