Геометрия Лобачевского не имеет столь простой и естественной интерпретации, как сферическая геометрия. Для геометрии Лобачевского известно несколько моделей.
В начале XX века почти одновременно несколько выдающихся математиков того времени — Карл Гаусс из Германии, Я. Бойяи из Венгрии и Николай Иванович Лобачевский из России пришли к мысли о существовании другой, неевклидовой геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную. Поскольку Н. И. Лобачевский первым высказал эту идею в 1826 году, новая неевклидова геометрия была названа в честь его имени.
Геометрия Лобачевского имеет лишь одно отличие от евклидовой — аксиома параллельности заменяется на ее отрицание — аксиому параллельности Лобачевского. Она так же нашла широчайшее применение в современной науке. Сам Николай Иванович Лобачевский использовал свою геометрию для вычисления определенных интегралов.
В теории функций комплексного переменного геометрия Лобачевского способствовала успешному построению теории автоморфных функций. В этой теории связь с геометрией Лобачевского была основой для исследований Пуанкаре. По словам Анри Пуанкаре «неевклидова геометрия есть ключ к решению всей задачи».
Кроме того, геометрия Лобачевского стала использоваться в теории чисел, а именно, в ее геометрических методах, так называемой «геометрии чисел». Ученые также установили тесную связь геометрии Лобачевского с кинематикой — специальной теорией относительности. В основе этой связи лежит равенство, выражающее закон распространения света.
В общей теории относительности геометрия Лобачевского также нашла свое место. Допуская тот факт, что распределение масс материи во Вселенной равномерно (это приближение в космических масштабах допустимо), то при определенных условиях пространство имеет геометрию Лобачевского. Тем самым было доказано предположение Лобачевского о новой геометрии как возможной теории пространства.
Теорема 1[1]. Пусть  выпуклый четырехугольник на плоскости Лобачевского (см. Рис. 8). Тогда следующие два свойства эквивалентны:
выпуклый четырехугольник на плоскости Лобачевского (см. Рис. 8). Тогда следующие два свойства эквивалентны:
(i) 
(ii) 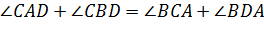 .
.

Рис. 8
Заметим, что каждое из свойств (i) и (ii) равносильно тому, что четырехугольник  является трапецией с основаниями
является трапецией с основаниями  и
и  . Вычитая из первого равенства второе, получим, что справедлива следующая лемма.
. Вычитая из первого равенства второе, получим, что справедлива следующая лемма.
Лемма 1[1]. Для трапеции  справедливо соотношение:
справедливо соотношение:
 .
.
В силу формулы Гаусса-Бонне [1] площади треугольников 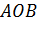 и
и  находятся по формулам:
находятся по формулам:
 ;
;
 .
.
Учитывая утверждение леммы и равенство вертикальных углов  , получим, что
, получим, что  .
.
Отсюда непосредственно заключаем, что имеют место равенства площадей  . Обозначим через
. Обозначим через  площадь гиперболического треугольника с длинами сторон
площадь гиперболического треугольника с длинами сторон  . Переписывая полученные два равенства в терминах длин сторон, установим, что справедливо следствие.
. Переписывая полученные два равенства в терминах длин сторон, установим, что справедливо следствие.
Следствие 1.1. Для площадей треугольников с соответствующими сторонами выполнены равенства:

| (2) |
Согласно работе [3] справедлива следующая формула для площади  гиперболического треугольника со сторонами
гиперболического треугольника со сторонами  :
:

| (3) |
Положим  и
и  . Подставляя равенство
. Подставляя равенство  в уравнение (3), получим, что система уравнений (2) эквивалентна следующей
в уравнение (3), получим, что система уравнений (2) эквивалентна следующей

| (4) |
Предложение 1. Длины сторон и диагонали трапеции связаны соотношениями

| (5) |
Из данной системы уравнений находятся выражения для длин диагоналей трапеции 

| (6) |

| (7) |
Сформулированное предложение потребуется для доказательства теоремы о площади трапеции.
Теорема 2[5]. Площадь  гиперболической трапеции
гиперболической трапеции  со сторонами
со сторонами  находится из соотношения
находится из соотношения

Евклидов вариант формулы, выражающий квадрат площади трапеции через ее стороны находится элементарными вычислениями из геометрических соображений и имеет вид:
 .
.
Отметим также, что 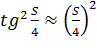 при достаточно малых величинах
при достаточно малых величинах  .
.
Доказательство. Рассмотрим трапецию  , изображенную на Рис. 1. Для вычисления ее площади воспользуемся формулой:
, изображенную на Рис. 1. Для вычисления ее площади воспользуемся формулой:
 .
.
Рассмотрим величину  . Учитывая равенство (1) из определения трапеции, получим, что
. Учитывая равенство (1) из определения трапеции, получим, что
 и
и  .
.
Откуда имеем

| (8) |
Выразим величины 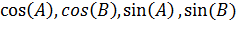 через длины сторон
через длины сторон  Воспользуемся теоремой косинусов для гиперболического треугольника
Воспользуемся теоремой косинусов для гиперболического треугольника  :
:
 .
.
Тогда для  имеем
имеем
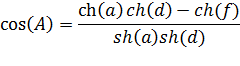
| (9) |
Для определения величины  через длины сторон
через длины сторон  подставим выражение
подставим выражение  в формулу (9) и, применив к ней соотношение (7), получим
в формулу (9) и, применив к ней соотношение (7), получим
 . .
| (10) |
Аналогично,
 . .
| (11) |
Вычислим выражение  используя приведенные выше формулы. После извлечения положительного квадратного корня, для величины
используя приведенные выше формулы. После извлечения положительного квадратного корня, для величины  имеем следующее выражение
имеем следующее выражение
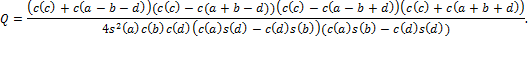
| (12) |
Подставляя в (8) результаты (10), (11), (12), после упрощения, получим

| (13) |
Далее,

| (14) |
Поделив (13) на (14), имеем утверждение теоремы
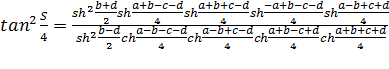 .
.
Что и требовалось доказать.
 2020-07-12
2020-07-12 127
127








