Площадь сферического двуугольника и треугольника

КУРСОВАЯ РАБОТА

по дисциплине: Гиперболическое многообразие

по теме: Площади неевклидовых многоугольников

                              

Научный руководитель:

к. ф-м. н., доцент

_______ Тулина М. И.

Работа защищена «__»___________2020 г.

с оценкой_____________

 

 

Горно-Алтайск, 2020 г.

Содержание

 

Введение. 3

1. Сферическая геометрия и неевклидова геометрия Римана. 5

2. Примеры теорем неевклидовой геометрии Римана. Площадь треугольника и многоугольника. 8

3. Геометрия Лобачевского. 13

4. Площадь многоугольников. 20

Заключение. 24

Список литературы.. 25

 

Введение

Первым неевклидовым геометром можно считать самого Евклида. Его нежелание использовать «несамоочевидный» пятый постулат следует хотя бы из того, что свои первые двадцать восемь предложений Евклид доказывает, не прибегая к этому постулату. С первого века до н.э. до 1820 математики пытались  вывести пятый постулат из остальных, но преуспели лишь в замене его различными эквивалентными допущениями такими как «две параллельные линии всюду равно удалены друг от друга» или «любые три точки, не расположенные на одной прямой, принадлежат окружности». Ближе всех подошел к цели логик и математик Дж. Саккери, который начал свои исследования с так называемого четырехугольника Саккери.

Саккери рассмотрел поочередно три гипотезы: верхние углы четырехугольника тупые, прямые и острые. Он доказал, что любая из этих гипотез, если ее принять для какого-нибудь одного такого четырехугольника, остается в силе для всех таких четырехугольников. Саккери намеревался обосновать гипотезу о том, что верхние углы прямые, доказав, что любая другая гипотеза приводит к противоречию. Вскоре он отверг гипотезу о тупом угле, и тем самым лишил себя возможности открыть эллиптическую геометрию, поскольку, как и все геометры до 1854, рассматривал второй постулат как утверждение о том, что прямая имеет бесконечную длину, и отказываться от этого постулата он не хотел. Точно так же Саккери в конце концов отверг и гипотезу об остром угле, но прежде, чем принять это ошибочное решение, он, сам того не ведая, открыл многие теоремы геометрии, получившей впоследствии название гиперболической.

К. Гаусса принято считать одним из величайших математиков всех времен. Он первым подошел к проблеме с современной точки зрения, согласно которой геометрию, отрицающую пятый постулат, надлежит развивать ради нее само, не ожидая, что при этом возникнет какое-то противоречие. Письма Гаусса к друзьям говорят о том, что к 1816 году он преодолел традиционный предрассудок относительно неизбежности противоречии, развил «антиевклидову» геометрию, удовлетворяющую гипотезе Саккери об остром угле. Но, опасаясь насмешек, он воздерживался от публикации этих идей и тем самым позволил разделить честь открытия гиперболической геометрии примерно в 1825 году венгру Я. Бойяи и русскому Н. И. Лобачевскому. Бойяи опубликовал свою работу до того, как услышал о Лобачевском. А сам, Лобачевский, судя по всему, так никогда и не узнал об исследованиях Бойяи. В 1854 Б. Риман заметил, что из неограниченности пространства еще не следует его бесконечная протяженность. Смысл этого утверждения станет яснее, если представить, что в неограниченной, но конечной вселенной астроном в принципе мог бы увидеть в телескоп, обладающий достаточно высокой разрешающей способностью, свой собственный затылок. В своем доказательстве того, что внешний угол при любой вершине треугольника больше внутреннего угла при любой из двух остальных вершин, Евклид неявно использовал бесконечную длину прямой. Из этой теоремы тотчас же следует теорема о том, что сумма любых двух углов треугольника меньше суммы двух прямых углов. Если отказаться от бесконечной длины прямой, то гипотеза Саккери о тупом угле становится верной и из нее следует, что сумма углов треугольника больше суммы двух прямых. Такое положение дела было давно известно в сферической тригонометрии, где стороны треугольника являются дугами больших кругов. Риман внес эпохальный вклад, распространив представление о конечном, но неограниченном пространстве с двух на три и большее число измерений.

Неевклидова геометрия — в буквальном понимании, любая геометрическая система, отличная от геометрии Евклида. Однако, традиционно термин «неевклидова геометрия» применяется в более узком смысле и относится только к двум геометрическим системам: геометрии Лобачевского и сферической геометрии.

Сферическая геометрия и неевклидова геометрия Римана

 

Огромное впечатление, произведенное на умы математиков открытием Лобачевского, Бойяи и Гаусса, быть может, было бы несколько менее сильным, если бы люди заметили, что еще задолго до Лобачевского они фактически уже владели содержательной геометрической схемой, отличной от традиционной геометрии Евклида, т. е. уже знали одну из неевклидовых геометрий. Однако твердое убеждение всех ученых в универсальности системы Евклида не позволило им оценить по достоинству тот запас знаний, которым они располагали. Именно поэтому первым примером геометрической системы, отличной от классической геометрии Евклида, считается обычно неевклидова геометрия Лобачевского. Значительно же более простая схема, по существу разработанная с большими деталями за много веков до Лобачевского, связывается обычно с именем гениального немецкого математика Бернхарда Римана, впервые обратившего внимание на родство этой схемы с классической геометрией Евклида и неевклидовой геометрией Лобачевского. Мы, однако, здесь не будем следовать истории вопроса и изложим более простую схему Римана до геометрии Лобачевского.

Когда говорим, что неевклидова геометрия Римана была известна задолго до открытия Лобачевского, имеем в виду тесную связь ее со сферической геометрией (геометрией на плоскости сферы). Основные факты сферической геометрии были основательно изучены еще в древности в связи с задачами астрономии. Поскольку поверхность земли приближенно имеет форму сферы, можно утверждать, что "земная геометрия" также является геометрией сферической.

Площадь сферического двуугольника и треугольника

 

Определение 1[5]. Всякая прямая разбивает сферу на две области-полусферы. Если провести две сферические прямые, то они разбивают сферу на четыре области, каждая из областей называется простым двуугольником.

На рис.1 изображены четыре двуугольника.

Рис. 1.

Среди всех сферических многоугольников наибольший интерес представляет сферический треугольник.

Определение 2[5]. При пересечении трёх больших окружностей получается сферический треугольник, причём таких треугольников на сфере образуется восемь.

Сторонами сферического треугольника являются отрезки сферических прямых , вершинами – их концы , углами – углы, образуемые сторонами сферического треугольника в его вершинах  (рис. 2).

Рис. 2

Пример 1. Найти площадь двуугольника 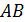с углом в  радиан (рис.3).

Рис. 3

Решение. Площадь сферы радиус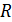а  равна , тогда площадь двуугольника с углом в один радиан будет равна . Отсюда искомая площадь равна .

Если нам дан сферический треугольник , то пара больших окружностей, проходящих через две его стороны, определяет два двуугольника, углы которых равны углу сферического треугольника между этими сторонами (рис. 2). Всего таким образом получается шесть двуугольников, два с углом , два – с углом 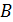 и два – с углом 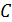. Треугольник  и диаметрально противоположный ему треугольник , равный треугольнику , входят в три двуугольника, остальные точки сферы, не лежащие на сторонах двуугольников,  входят только в один двуугольник. Поэтому сумма площадей шести двуугольников равна сумме площади  всей сферы и учетверенной , то есть .

Так как , то мы получаем

,

то есть . Так как величины  и  положительны, то величина  также положительна, откуда следует, что , т.е. сумма углов сферического треугольника больше развёрнутого угла. Величина  называется угловым избытком сферического треугольника. Таким образом, площадь сферического треугольника равна произведению его углового избытка на квадрат радиуса сферы.