Удельная поверхностная мощность

Излучаемая индуктором электромагнитная волна падает на металлическое тело и, поглощаясь в нем, вызывает нагрев.

Мощность потока энергии, протекающего через единицу поверхности тела, определяется формулой (2.1)

 

,

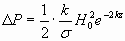(2.1)

 

Удельную мощность на поверхности тела можно получить, подставив, в приведенное выражение

z = 0;

 

 

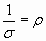
и значение k из формулы

 

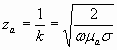
(2.2)

с учетом выражения

 

.

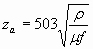(2.3)

 

После преобразования получаем (Вт/м²):

 

,

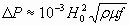(2.4)

 

В практических расчетах пользуются размерностью D Р в Вт/см², тогда:

 

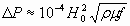,	(2.5)

где Н₀ -в А/см;

r - в Ом×см.

Величина 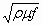носит название коэффициента поглощения мощности.

Выразим D Р через ампер-витки индуктора. С известным приближением напряженность магнитного поля H₀ можно представить в виде произведения действующего значения тока индуктора I и числа витков w ₀ на 1 см его высоты:

 

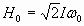,	(2.6)

Подставив полученное значение H ₀ в формулу (207), получим

 

.

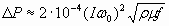(2.7)

 

Таким образом, мощность, выделяемая в изделии, пропорциональна квадрату ампер-витков индуктора и коэффициенту поглощения мощности. При неизменной напряженности магнитного поля интенсивность нагрева тем больше, чем больше удельное сопротивление r, магнитная проницаемость материала m и частота тока f.

 

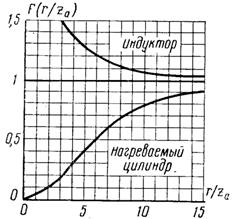
Рис. 2.3– Функции Берча для вычисления мощности у поверхности индуктора, выделяющейся в нагреваемом цилиндре и индукторе

 

Формула (2.7) справедлива для плоской электромагнитной волны.

При нагреве цилиндрических тел в соленоидных индукторах картина распространения волн усложняется.

Отклонения от соотношений для плоской волны тем больше, чем меньше отношения r/z_а,

где r -радиус цилиндра,

  z_а - глубина проникновения токов.

В практических расчетах все же пользуются простой зависимостью (2.7), вводя в нее поправочные коэффициенты - функции Берча, зависящие от отношения r/z_а (рис. 2.3). Тогда

,

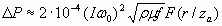(2.8)