Гармонические колебания

1 Уравнение гармонических колебаний:

где x – смещение (отклонение от состояния равновесия) колеблющейся величины, описывающий тот или иной физический процесс; А – амплитуда колебаний; (w t + j₀) - фаза колебаний; j₀ – начальная фаза; – круговая или циклическая частота; n = 1/ T – линейная частота.

2 Скорость и ускорение точки, совершающей гармонические колебания

3 Энергия гармонических колебаний

Кинетическая энергия колеблющейся точки массой m

Потенциальная энергия

Полная энергия гармонического колебания

4 Дифференциальное уравнение простейшей колебательной системы (гармонического осциллятора)

5 Пружинный, математический и физический маятники

Период колебаний пружинного маятника

где m – масса маятника; k – жёсткость пружины.

Период колебаний математического маятника

где l – длина нити маятника; g – ускорение свободного падения.

Период колебаний физического маятника

где J – момент инерции маятника относительно оси колебаний; l – расстояние от центра масс маятника до оси колебания; – приведённая длина физического маятника.

6 Колебательный контур

Период колебаний колебательного контура (формула Томсона)

где L – индуктивность; С – электроёмкость контура.

Энергия колебательного контура

ВОЛНЫ В УПРУГОЙ СРЕДЕ

1 Уравнение плоской бегущей волны, распространяющейся вдоль положительного направления оси x

x(x, t)= A cos [w(t - x/V) + j₀] или x(x, t)= A cos (w t - kx + j₀),

где x(x, t) – смещение точек среды с координатой х в момент времени t;

А – амплитуда; (w t - kx + j₀)– фаза; j₀– начальная фаза; w – круговая частота; V – скорость распространения колебаний в среде (фазовая скорость); k – волновое число (k =2p /l, l – длина волны).

2 Связь длины волны с периодом и частотой

l = V×T и ,

где Т – период колебаний точек волны; v – частота.

3 Разность фаз колебаний двух точек среды

где D x – расстояние между колеблющимися точками (разность хода); l – длина волны.

4 Фазовая скорость волны

а) продольных волн (распространяющихся в упругой среде и твердых телах)

где Е – модуль Юнга; 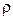– плотность вещества;

б) поперечных волн

где G – модуль сдвига;

в) волн в газах

где g – показатель адиабаты (); R – универсальная газовая постоянная; Т – термодинамическая температура; m – молярная масса газа.

5 Уравнение стоячей волны

x (x,t) = 2 A cos w t cos kx.

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

1 Уравнение плоской электромагнитной волны

= ₀cos (w t – kx + j₀),

где ₀ и ₀ - соответственно амплитуды напряженности электрического и магнитного полей волны.

2 Скорость распространения электромагнитной волны

где e - диэлектрическая проницаемость среды; e₀– электрическая постоянная; m -магнитная проницаемость среды; m₀ – магнитная постоянная; e₀ = 8.85×10^–12 Ф/м; m₀ =12,566 × 10^–7 Гн/м. Для вакуума e = 1; m = 1; V = с = 3×10⁸ м/с.

3 Плотность энергии электромагнитной волны