1 Сила тока
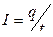 ,
,
где q – заряд, прошедший через поперечное сечение проводника за время t.
Плотность тока:
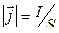 ,
,
где S – площадь поперечного сечения проводника, а направление вектора плотности тока совпадает с направлением силы тока.
2 Закон Ома:
а) 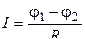 или
или 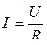 (для участка цепи, не содержащего э.д.с.),
(для участка цепи, не содержащего э.д.с.),
где j1 – j2 = U – разность потенциалов (напряжение) на концах участка цепи; R – сопротивление участка;
б) 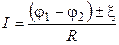
 (для участка цепи, содержащего э.д.с.), где x– э.д.с. источника тока; R – полное сопротивление участка (сумма внешних и внутренних сопротивлений);
(для участка цепи, содержащего э.д.с.), где x– э.д.с. источника тока; R – полное сопротивление участка (сумма внешних и внутренних сопротивлений);
в) 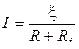 (для замкнутой цепи), где R – внешнее сопротивление цепи; Ri – внутреннее сопротивление цепи (сопротивление источника тока).
(для замкнутой цепи), где R – внешнее сопротивление цепи; Ri – внутреннее сопротивление цепи (сопротивление источника тока).
3 Сопротивление проводника: 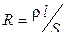 , где r – удельное сопротивление; l – длина проводника; S – площадь поперечного сечения проводника.
, где r – удельное сопротивление; l – длина проводника; S – площадь поперечного сечения проводника.
Сопротивление системы проводников: a) 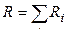 (при последовательном соединении); б)
(при последовательном соединении); б) 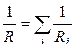 (при параллельном соединении), где Ri – сопротивление i -го проводника.
(при параллельном соединении), где Ri – сопротивление i -го проводника.
4 Работа, совершаемая электрическим током:
A = I U t, A = I 2 R t, 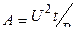 .
.
Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение U, последние две – для участка, не содержащего э.д.с.
5 Мощность электрического тока:
P = I U, P = I 2 R, 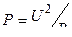 .
.
6 Закон Джоуля – Ленца: Q = I 2R t = I U t,
где Q – количество теплоты, выделяющейся в проводнике за время t при прохождении по нему постоянного тока I.
7 Закон Ома в дифференциальной форме:
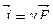 ,
,
где 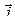 – плотность тока; g – удельная проводимость;
– плотность тока; g – удельная проводимость; 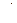 - напряженность электрического поля.
- напряженность электрического поля.
ЭЛЕКТРОМАГНЕТИЗМ
1 Закон Био – Савара – Лапласа:
 , или
, или 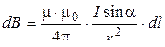 ,
,
где 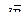 – индукция магнитного поля, создаваемого элементом проводника длиной
– индукция магнитного поля, создаваемого элементом проводника длиной 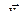 с током I;
с током I; 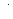 – радиус-вектор, проведенный из этого элемента проводника в ту точку поля, в которой вычисляется магнитная индукция;
– радиус-вектор, проведенный из этого элемента проводника в ту точку поля, в которой вычисляется магнитная индукция; 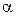 – угол между радиус-вектором
– угол между радиус-вектором 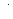 и направлением тока в элементе проводника; μ – относительная магнитная проницаемость изотропной среды (для вакуума μ = 1); μ0 – магнитная постоянная (μ0 = 4π·10-7 Гн/м).
и направлением тока в элементе проводника; μ – относительная магнитная проницаемость изотропной среды (для вакуума μ = 1); μ0 – магнитная постоянная (μ0 = 4π·10-7 Гн/м).
2 Магнитная индукция поля, созданного произвольной системой
проводников с токами (принцип суперпозиции магнитных полей):
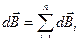 ,
,
где 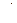 – магнитная индукция результирующего поля;
– магнитная индукция результирующего поля; 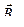 – магнитные индукции
– магнитные индукции 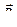 ,...,
,..., 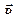 складываемых полей.
складываемых полей.
3 Магнитная индукция в центре кругового тока:
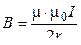 ,
,
где r – радиус кругового витка с током.
4 Магнитная индукция на оси кругового тока:
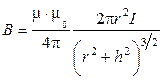 ,
,
где h – расстояние от центра витка с током до точки, в которой вычисляется магнитная индукция.
5 Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током:
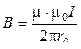 ,
,
где r 0 – кратчайшее расстояние от оси проводника до точки, в которой вычисляется магнитная индукция.
6  Магнитная индукция поля, создаваемого прямолинейным проводником с током в произвольной точке (рисунок а):
Магнитная индукция поля, создаваемого прямолинейным проводником с током в произвольной точке (рисунок а):
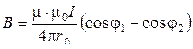 ,
,
где φ1, φ2 – углы, образованные прямыми, проведенными из рассматриваемой точки к концам проводника, и направлением тока, проходящего через проводник. При симметричном расположении концов проводника относительно точки, в которой определяется магнитная индукция (рисунок б), -cosφ2 = cosφ1 = cosφ, тогда:  . Вектор магнитной индукции
. Вектор магнитной индукции 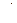 перпендикулярен плоскости чертежа, направлен к нам и поэтому изображен точкой.
перпендикулярен плоскости чертежа, направлен к нам и поэтому изображен точкой.
7 Циркуляция вектора напряженности магнитного поля вдоль замкнутого контура:
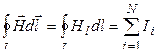 ,
,
где 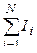 – алгебраическая сумма токов, охватываемых данным контуром. Знак "+" у тока берется в случае, если направление обхода контура и направление тока составляют правовинтовую систему.
– алгебраическая сумма токов, охватываемых данным контуром. Знак "+" у тока берется в случае, если направление обхода контура и направление тока составляют правовинтовую систему.
8 Циркуляция вектора магнитной индукции вдоль замкнутого контура:
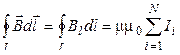 .
.
9 Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на его оси):
B = μ μ0 n I.
где n= 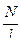 – число витков, приходящихся на единицу длины соленоида.
– число витков, приходящихся на единицу длины соленоида.
10 Связь магнитной индукции 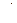 с напряженностью
с напряженностью  магнитного поля:
магнитного поля:
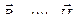 , или
, или 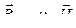 (в вакууме).
(в вакууме).
11 Закон Ампера:
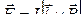 , или F = B I l sinα,
, или F = B I l sinα,
где  – сила, действующая на прямой отрезок проводника с током I, помещенный в однородное магнитное поле; l – длина проводника; α – угол между направлением тока в проводнике и вектором магнитной индукции
– сила, действующая на прямой отрезок проводника с током I, помещенный в однородное магнитное поле; l – длина проводника; α – угол между направлением тока в проводнике и вектором магнитной индукции 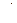 . Если поле неоднородно и проводник не является прямым, то закон Ампера можно применять к каждому элементу проводника в отдельности:
. Если поле неоднородно и проводник не является прямым, то закон Ампера можно применять к каждому элементу проводника в отдельности:
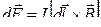 , или dF = B I dl sinα.
, или dF = B I dl sinα.
12 Сила взаимодействия двух бесконечно длинных параллельных
проводников с током:
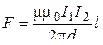 ,
,
где d – расстояние между проводниками.
13 Магнитный момент контура с током:
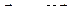 , или p = I S,
, или p = I S,
где I – сила тока в плоском контуре; S – площадь, охватываемая контуром; 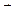 – единичный вектор положительной нормали к плоскости контура. Вектор магнитного момента
– единичный вектор положительной нормали к плоскости контура. Вектор магнитного момента 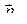 направлен перпендикулярно плоскости контура в соответствии с правилом буравчика.
направлен перпендикулярно плоскости контура в соответствии с правилом буравчика.
14 Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле:
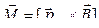 , или M = p m B sinα,
, или M = p m B sinα,
где α – угол между векторами 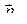 и
и 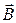 .
.
15 Потенциальная энергия контура с током в магнитном поле:
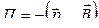 , или П = - pm B cosα.
, или П = - pm B cosα.
За нулевое значение потенциальной энергии контура с током в магнитном поле принято расположение контура, когда вектор 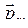 перпендикулярен вектору
перпендикулярен вектору 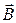 .
.
16 Отношение магнитного момента p m к механическому моменту L (моменту импульса) заряженной частицы, движущейся по круговой орбите:
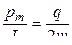 ,
,
где q – заряд частицы; m – масса частицы.
17 Сила Лоренца:
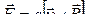 , или
, или 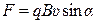 ,
,
где 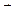 – скорость заряженной частицы; a – угол между векторами
– скорость заряженной частицы; a – угол между векторами 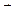 и
и 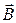 .
.
18 Если частица находится одновременно в электрическом и магнитном полях, то под силой Лоренца понимают выражение:
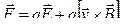 ,
,
где  – вектор напряженности электрического поля.
– вектор напряженности электрического поля.
19 Магнитный поток: а) в случае однородного магнитного поля и плоской поверхности:
Ф = B S cos a, или Ф = Bn S,
где Bn = B cos a – проекция вектора 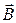 на направление нормали к площадке; S – площадь контура; a – угол между нормалью к плоскости контура и вектором магнитной индукции;
на направление нормали к площадке; S – площадь контура; a – угол между нормалью к плоскости контура и вектором магнитной индукции;
б) в случае неоднородного магнитного поля и произвольной поверхности:
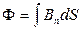 ,
,
интегрирование ведется по всей поверхности.
20 Теорема Гаусса:
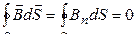 ,
,
где 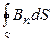 – магнитный поток через замкнутую поверхность.
– магнитный поток через замкнутую поверхность.
21 Потокосцепление (полный магнитный поток):
Ψ = N Ф,
где Ф – магнитный поток через один виток; N – число витков. Эта формула применима для вычисления Ψ соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу витков.
22 Работа сил Ампера при перемещении проводника с током в магнитном поле:
A = I Δ Ф,
где Δ Ф – магнитный поток, пересекаемый проводником при его движении.
23 Работа сил Ампера при перемещении замкнутого контура с током в магнитном контуре:
А = I Δ Ф = I (Ф2 - Ф1),
где Δ Ф – изменение магнитного потока, пронизывающего контур.
24 Э.д.с. индукции:
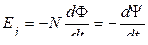 ,
,
где N – число витков контура; Ψ – потокосцепление. Знак минус указывает, что э.д.с. индукции (или ток индукции), согласно правилу Ленца, противодействует изменению магнитного потока, пронизывающего контур.
25 Разность потенциалов на концах проводника, движущегося со скоростью 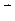 в магнитном поле:
в магнитном поле:
U = B l 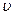 sinα,
sinα,
где l – длина проводника; α – угол между векторами 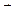 и
и 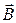 .
.
26 Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур:
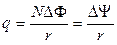 ,
,
где r – сопротивление контура.
27 Индуктивность контура:
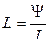 .
.
28 Э.д.с. самоиндукции:
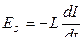 .
.
29 Индуктивность соленоида:
L= μμ0 n 2 V,
где n – число витков, приходящееся на единицу длины соленоида; V – объем соленоида.
30 Энергия магнитного поля:
W=L I 2 / 2.
31 Объемная плотность энергии магнитного поля (энергия, заключенная в единице объема):
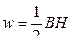 , или
, или 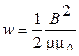 , или
, или 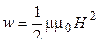 ,
,
где B – магнитная индукция; H – напряженность магнитного поля.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
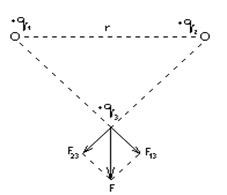
1 Два равных по величине заряда 3 × 10-9 Кл расположены в вершинах при острых углах равнобедренного прямоугольного треугольника на расстоянии  см. Определить, с какой силой эти два заряда действуют на третий заряд +1 × 10-9 Кл, расположенный в вершине при прямом угле треугольника. Рассмотреть случай, когда первые два заряда одно- и разноименные, и пояснить их рисунками.
см. Определить, с какой силой эти два заряда действуют на третий заряд +1 × 10-9 Кл, расположенный в вершине при прямом угле треугольника. Рассмотреть случай, когда первые два заряда одно- и разноименные, и пояснить их рисунками.
Решение
 Сила взаимодействия между двумя точечными зарядами определяется по закону Кулона:
Сила взаимодействия между двумя точечными зарядами определяется по закону Кулона: 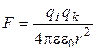 . По принципу суперпозиции поле каждого заряда q 1и q 2действует на заряд q 3независимо. Вследствие этого на заряд q 3 действуют независимо силы
. По принципу суперпозиции поле каждого заряда q 1и q 2действует на заряд q 3независимо. Вследствие этого на заряд q 3 действуют независимо силы 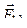 и
и 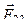 .
.
|
|
Векторная сумма этих сил 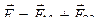 будет искомой величиной. Как видно из рисунка, сила
будет искомой величиной. Как видно из рисунка, сила  в обоих случаях будет одинаковой по абсолютной величине. Перейдем от векторного к скалярному выражению сил. Введем обозначение F 13 = F 23 = F 3. Тогда из геометрических соображений
в обоих случаях будет одинаковой по абсолютной величине. Перейдем от векторного к скалярному выражению сил. Введем обозначение F 13 = F 23 = F 3. Тогда из геометрических соображений 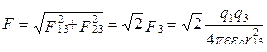 , где r 13 (или r 23) - расстояние между зарядами q 1 и q 3 и (или) q 2 и q 3, r 13 = r 23 = r /
, где r 13 (или r 23) - расстояние между зарядами q 1 и q 3 и (или) q 2 и q 3, r 13 = r 23 = r / 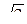 .
.
Подставляя числовые значения, определим F = 9,5 × 10-5 Н.
2 Два одинаковых положительных заряда 10-12 Кл находятся в воздухе на расстоянии 8 см друг от друга. Определить напряженность поля и потенциал в точке, расположенной на расстоянии 5 см от зарядов.
Решение
 По принципу суперпозиции напряженность поля, создаваемого зарядами q 1и q 2, равна векторной сумме напряженностей, создаваемых каждым зарядом в данной точке поля:
По принципу суперпозиции напряженность поля, создаваемого зарядами q 1и q 2, равна векторной сумме напряженностей, создаваемых каждым зарядом в данной точке поля: 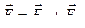 . Напряженность поля, создаваемого точечным зарядом, вычисляется по формуле
. Напряженность поля, создаваемого точечным зарядом, вычисляется по формуле
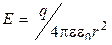 , (2.1)
, (2.1)
где q – заряд; e – диэлектрическая проницаемость; e0 – электрическая постоянная; r – расстояние от заряда до точки поля, в которой определяется напряженность.
Так как заряды q 1 и q 2положительны, то векторы 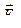 и
и 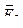 имеют направление по силовой линии от заряда. Как видно из рисунка, вектор суммарной напряженности
имеют направление по силовой линии от заряда. Как видно из рисунка, вектор суммарной напряженности  является диагональю параллелограмма со сторонами
является диагональю параллелограмма со сторонами 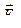 и
и 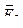 . Его абсолютное значение находим, используя теорему косинусов
. Его абсолютное значение находим, используя теорему косинусов
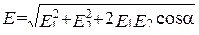 , (2.2)
, (2.2)
где a - угол между векторами 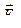 и
и 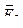 , который можно определить из треугольника со сторонами r 1, r 2и r 3:
, который можно определить из треугольника со сторонами r 1, r 2и r 3:
 .
.
Подставляя 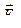 и
и 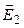 из (2.1) в (2.2), после преобразований получаем
из (2.1) в (2.2), после преобразований получаем
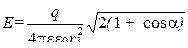 (2.3)
(2.3)
Потенциал j, создаваемый в данной точке поля системой точечных зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности: 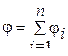 . В данной задаче потенциал j результирующего поля будет равен j = j1 + j2 Потенциал, создаваемый точечным зарядом, определяется по формуле
. В данной задаче потенциал j результирующего поля будет равен j = j1 + j2 Потенциал, создаваемый точечным зарядом, определяется по формуле 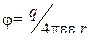 . Следовательно, потенциал результирующего поля
. Следовательно, потенциал результирующего поля
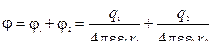 . (2.4)
. (2.4)
Подставляя числовые значения в формулы (2.3) и (2.4), находим напряженность поля и потенциал: Е = 4,32 В/м; j = 0,39 В.
3 Определить ускоряющую разность потенциалов U, которую должен пройти в электрическом поле электрон, обладающий скоростью v1 =106 м/с, чтобы скорость его возросла в 2 раза.
Решение
Ускоряющую разность потенциалов можно найти, вычислив работу А сил электростатического поля. Эта работа определяется произведением заряда е электрона на разность потенциалов U:
A = eU. (3.1)
Работа сил электростатического поля в данном случае равна изменению кинетической энергии электрона:
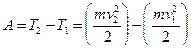 , (3.2)
, (3.2)
где T 1и T 2 – кинетические энергии электрона до и после прохождения ускоряющего поля; m – масса электрона; v 1и v 2 – начальная и конечная его скорости. Приравняв правые части равенств (3.1) и (3.2), получим
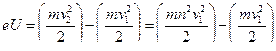 , (3.3)
, (3.3)
где n = v 2 / v 1 = 2. Отсюда искомая разность потенциалов
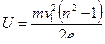 . (3.4)
. (3.4)
Подставив числовые значения, получим: U = 8,53 В.
4. Между пластинами плоского конденсатора, находящимися на расстоянии 1 см, приложена разность потенциалов 200В. К одной из пластин прилегает плоскопараллельная стеклянная пластина (e1= 7) толщиной 9 мм. Конденсатор отключают от источника напряжения и после этого вынимают пластину. Определить разность потенциалов между пластинами конденсатора. Во сколько раз изменится энергия конденсатора?
Решение
Разность потенциалов между пластинами конденсатора в случае отключения его от источника напряжения находится из условия, что заряд на его пластинах остается неизменным, т.е.
C 1 U 1 = C 2 U 2, (4.1)
где C 1и C 2 - емкости конденсатора; U 1и U 2 - разности потенциалов.
В условиях данной задачи конденсатор вначале является слоистым и его емкость C 1находится по формуле для определения емкости батареи последовательно соединенных конденсаторов:
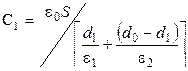 , (4.2)
, (4.2)
где S - площадь пластин; e1 и e2 - диэлектрические проницаемость стекла и воздуха; d 1 - толщина стеклянной пластины; d 0 - зазор между пластинами.
После удаления стеклянной пластины из зазора конденсатор становится простейшим плоским конденсатором с емкостью
 . (4.3)
. (4.3)
Разность потенциалов U 2, которая устанавливается после удаления из зазора стеклянной пластины, определим из формулы (4.1), подставляя в нее (4.2) и (4.3) и производя соответствующие преобразования:
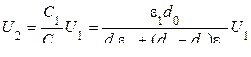 . (4.4)
. (4.4)
Подставим числовые значения в (4.4), получаем U 2= 976 В.
Энергия конденсатора равна
W = CU 2/2.
Изменение энергии конденсатора найдем, узнав отношение энергии конденсаторов:
W 2 / W 1 = C 2 U 22 / (C 1 U 12 ). (4.5)
Отношение (4.5) можно представить в виде
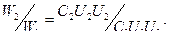
Так как по условию C 1 U 1 = C 2 U 2, то
W 2 / W 1 = U 2 / U 1= 4,38.
5. Определить максимальную мощность, которая может выделяться во внешней цепи, питаемой от батареи с э.д.с. 12 В, если наибольшая сила тока, которую может дать батарея, равна 5 А.
Решение
Используем закон Ома для замкнутой цепи
|
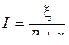 , (5.1)
, (5.1)
где R - сопротивление внешней цепи; r - внутреннее сопротивление источника тока.
Мощность тока P, выделяемая во внешней цепи, определяется по формуле N= I 2 R. Преобразуем это выражение, используя (5.1):
 . (5.2)
. (5.2)
Таким образом, мощность зависит от сопротивления внешней цепи R. Мощность будет максимальной при таком значении R, при котором первая производная 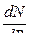 обращается в нуль.
обращается в нуль.
Возьмем первую производную
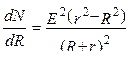 . (5.3)
. (5.3)
Из (5.3) видно, что 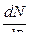 = 0 при R=r. Определим r. Максимальный ток возникает при коротком замыкании цепи, т.е. когда внешнее сопротивление R =0. Исходя из этого,
= 0 при R=r. Определим r. Максимальный ток возникает при коротком замыкании цепи, т.е. когда внешнее сопротивление R =0. Исходя из этого, 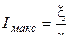 , откуда
, откуда 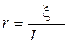 , а значит,
, а значит,
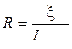 . (5.4)
. (5.4)
Подставив (5.4) и (5.2) и выполнив преобразования, получим
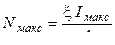 . (5.5)
. (5.5)
После вычислений получим: N = 15 Bт.
6. Потенциометр с сопротивлением R =100 Ом подключен к батарее, э.д.с. которой x= 150 В и внутреннее сопротивление r =50 Ом. Определить:
1) показание вольтметра с сопротивлением Rв =500 Ом, соединенного с одной из клемм потенциометра и подвижным контактом, установленным посередине потенциометра;
2) разность потенциалов между теми же точками потенциометра при отключении вольтметра.
Решение
1. Показание вольтметра, подключенного к точкам А и В как показано на рисунке, определим по формуле
U 1 =I 1 R 1, (6.1)
где R 1- суммарное сопротивление вольтметра и потенциометра, которые соединены параллельно; I 1 - сила тока в ветвях этого соединения.
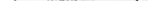 Силу тока I 1 найдем по закону Ома для полной цепи:
Силу тока I 1 найдем по закону Ома для полной цепи:
I 1 =x / (Re+r), (6.2)
где Re сопротивление внешней цепи. Это сопротивление есть сумма двух сопротивлений
Re= R/2+ R 1 . (6.3)
 Сопротивление R 1 найдем по формуле параллельного соединения проводников
Сопротивление R 1 найдем по формуле параллельного соединения проводников 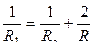 , откуда
, откуда
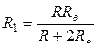 . (6.4)
. (6.4)
Подставив в (6.2) выражение Re по (6.3), найдем
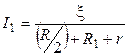 . (6.5)
. (6.5)
В данном случае решение задачи в общем виде было бы громоздким. Поэтому удобно вычисления величин провести раздельно: R 1 = 45,5 Ом; I 1=1,03 A; U 1 = 46,9 В.
2. Разность потенциалов между точками A и B при отключенном вольтметре равна произведению силы тока I 2 на половину сопротивления потенциометра:
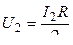 , (6.6)
, (6.6)
где I 2 - сила тока в цепи при отключенном вольтметре. Ее определим по формуле
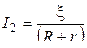 .
.
Подставив выражение для I 2 в формулу (6.6), найдем
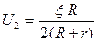 .
.
Произведем вычисления: U 2= 50 B.
Таким образом, в результате вычислений мы получили: 1) U 1 = 46,9 В; 2) U 2= 50 B.
7 По проводнику, согнутому в виде квадратной рамки со стороной а = 10 см, течет ток I = 5 А. Определить индукцию В магнитного поля в точке, равноудаленной от вершин квадрата на расстояние, равное его стороне.
Решение

 Искомая индукция
Искомая индукция 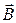 магнитного поля в точке Аявляется векторной суммой индукций
магнитного поля в точке Аявляется векторной суммой индукций 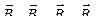 , создаваемых в этой точке токами, текущими в каждом из четырех проводов, являющихся сторонами квадрата. Из соображений симметрии все четыре индукции по абсолютной величине равны между собой. На рисунке изображен только один из четырех векторов
, создаваемых в этой точке токами, текущими в каждом из четырех проводов, являющихся сторонами квадрата. Из соображений симметрии все четыре индукции по абсолютной величине равны между собой. На рисунке изображен только один из четырех векторов 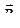 , соответствующий полю, создаваемому током в проводе DC. B соответствии с правилом буравчика вектор
, соответствующий полю, создаваемому током в проводе DC. B соответствии с правилом буравчика вектор 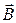 перпендикулярен плоскости треугольника ADC. Геометрическая сумма
перпендикулярен плоскости треугольника ADC. Геометрическая сумма  будет направлена вдоль оси OO и равна сумме проекций всех векторов на направление этой оси, т.е. В = 4 В 1 cosa. Из рисунка следует, что cosa =
будет направлена вдоль оси OO и равна сумме проекций всех векторов на направление этой оси, т.е. В = 4 В 1 cosa. Из рисунка следует, что cosa = 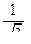 , и тогда
, и тогда
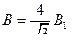 , (7.1)
, (7.1)
Индукция магнитного поля, создаваемого отрезком проводника, выражается формулой
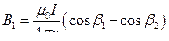 , (7.2)
, (7.2)
где I – сила тока в проводнике; r – расстояние от проводника до точки, в которой надо определить напряженность поля; b1 и b2 - углы, образованные направлением тока в проводнике и радиус-векторами, проведенными от концов проводника к точке А.
В нашем случае b2 = p – b1, следовательно, cos b2 = – cos b1, и выражение (7.2) приобретает вид
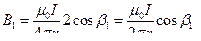 .
.
Подставляем выражение для В1 в формулу (7.1):
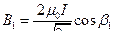 . (7.3)
. (7.3)
Заметим, что 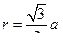 (a – длина стороны квадрата) и что
(a – длина стороны квадрата) и что  , так как b1 =60° как угол равностороннего треугольника. С учетом этого перепишем выражение (7.3) в окончательном виде
, так как b1 =60° как угол равностороннего треугольника. С учетом этого перепишем выражение (7.3) в окончательном виде
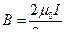 .
.
Подставив числовые значения, получим: В = 13,3 мкТл.
8 Электрон, пройдя ускоряющую разность потенциалов U = 400 В, попал в однородное магнитное поле с индукцией В = 1,5 мТл. Определить радиус кривизны траектории R и частоту n обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля.
Решение
1) Радиус кривизны траектории электрона определим, исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца F, а действием силы тяжести можно пренебречь. Сила Лоренца перпендикулярна к вектору скорости и, следовательно, является в данном случае центростремительной силой, т. е. F = Fцс. Подставляя выражения для F и F цс, получим
 , (8.1)
, (8.1)
где е - заряд электрона; 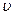 - скорость электрона; В - индукция магнитного поля; m - масса электрона; R - радиус кривизны траектории; a – угол между направлениями вектора скорости
- скорость электрона; В - индукция магнитного поля; m - масса электрона; R - радиус кривизны траектории; a – угол между направлениями вектора скорости 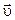 и вектора индукции
и вектора индукции 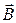 (в нашем случае
(в нашем случае 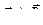 и a = 90°, sin a = 1). Далее найдем:
и a = 90°, sin a = 1). Далее найдем:
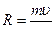 . (8.2)
. (8.2)
Входящий в выражение (8.2) импульс mu может быть выражен через кинетическую энергию Т электрона
 . (8.3)
. (8.3)
Но кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством T = eU. Подставив Т в формулу (6.3), получим:  . Учитывая это, выражение (6.2) для радиуса кривизны приобретает вид:
. Учитывая это, выражение (6.2) для радиуса кривизны приобретает вид:
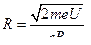 .
.
2) Для определения частоты обращения электрона воспользуемся формулой, связывающей частоту со скоростью и радиусом кривизны траектории:
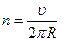 .
.
Подставив в эту формулу выражение (6.2) для радиуса кривизны, получим
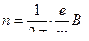 .
.
Подставим численные значения и произведем вычисления. В результате получим:1) R = 4,41 × 10–2 м, 2) n = 4,21 × 107 об/с.
 2020-07-12
2020-07-12 94
94