2020-06-29
500
Методы решения логарифмических уравнений.
По определению логарифма;
• Метод потенцирования (освобождения от знака логарифма);
• Решение уравнений с использованием свойств логарифмов;
• Метод введения новой переменной;
• Логарифмирование уравнений;
• Другие методы (функционально-графический, метод приведения к одному основанию).
Рассмотрим каждый метод более подробно:
По определению логарифма.
По определению логарифма решаются простейшие уравнения вида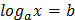 
.
.
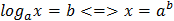Пример 1. Решить уравнение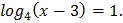 
Решение: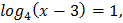 
ОДЗ: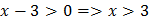 
,
Используем определение логарифма:
,
,
.
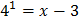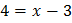Ответ: .
Пример 2. Решить уравнение 
,
Решение: ,
ОДЗ: 
.
По определению логарифма:
,
,
,
.
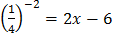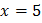Ответ: .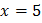
Метод потенцирования (освобождения от знака логарифма).
Решение логарифмического уравнения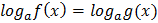 
основано на том, что данное уравнение равносильно уравнению 
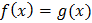при дополнительных условиях
.
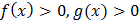Пример 3. Решить уравнение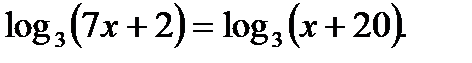 
Решение:
ОДЗ: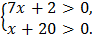 
< 
.
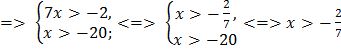Потенцируя получим:
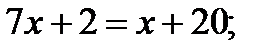
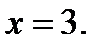
Ответ: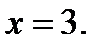
Решение уравнений с использованием свойств логарифмов.
Пример 4. Решить уравнение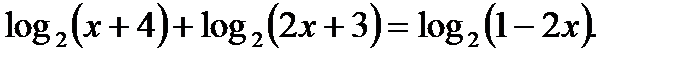 
Решение:
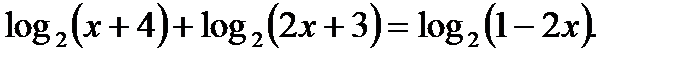
ОДЗ: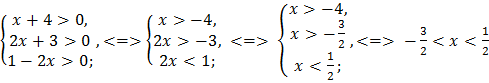 
.
Вспомним свойства логарифмов – сумма логарифмов двух положительных чисел равна логарифму произведения этих чисел, поэтому: 
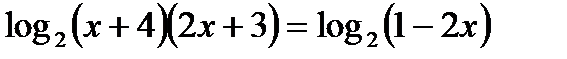
Освободимся от знака логарифма и решим квадратное уравнение:
,
,
, 
.
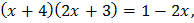
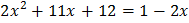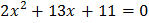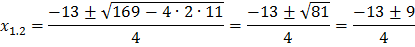
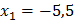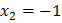Согласовав корни с ОДЗ, получим корень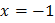 
.
Ответ: .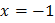
Метод введения новой переменной.
Пример 5. Решить уравнение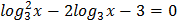 
Решение:
ОДЗ: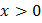 
В данном уравнении повторяется выражение: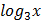 
. Значит можно выполнить замену переменной.
Пусть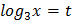 
. Тогда уравнение примет вид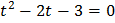 
Возвратимся к исходной переменной. Остается решить простейшие логарифмические уравнения:
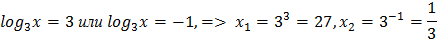
Ответ: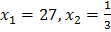 
.
При решении логарифмических уравнений, возможно появление посторонних корней. Причина их появления — расширение области определения исходного уравнения. Поэтому проверка корней логарифмического уравнения осуществляется либо по области определения, либо непосредственной подстановкой найденных корней в исходное логарифмическое уравнение.
Тригонометрические уравнения. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическими.
