Дифференциальное уравнение  го порядка имеет вид
го порядка имеет вид  .
.
Если это уравнение решить относительно  то оно может быть представлено в виде
то оно может быть представлено в виде 
Определение. Решением ДУ на интервале  называется всякая функция
называется всякая функция  , зависящая от
, зависящая от  произвольных постоянных
произвольных постоянных  и такая, что подстановка
и такая, что подстановка  и ее производных в дифференциальное уравнение обращает последнее на интервале
и ее производных в дифференциальное уравнение обращает последнее на интервале  в тождество по
в тождество по  .
.
Задача Коши: задача отыскания решения  дифференциального уравнения, удовлетворяющего заданным начальным условиям
дифференциального уравнения, удовлетворяющего заданным начальным условиям  ,
,  , ………….
, ………….  .
.
Теорема. Если функция  непрерывна по совокупности аргументов, имеет непрерывные производные
непрерывна по совокупности аргументов, имеет непрерывные производные 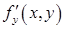 ,
,  ,
,  , …,
, …,  в некоторой области, содержащей точку
в некоторой области, содержащей точку  , то существует и притом единственное решение задачи Коши.
, то существует и притом единственное решение задачи Коши.
Определение. Пусть выполняются условия предыдущей теоремы.
Общим решением дифференциального уравнения 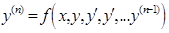 в некоторой области
в некоторой области 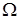 существования и единственности решения задачи Коши называется функция
существования и единственности решения задачи Коши называется функция  , зависящая от переменной
, зависящая от переменной  и
и  постоянных
постоянных  , такая, что:
, такая, что:
а) при любых допустимых значениях постоянных  функция
функция  является решением уравнения;
является решением уравнения;
б) при заданных начальных условиях постоянные  всегда можно подобрать так, что функция
всегда можно подобрать так, что функция  будет удовлетворять этим условиям.
будет удовлетворять этим условиям.
В процессе интегрирования дифференциального уравнения часто приходят к уравнению  , неявно задающему общее решение уравнения. Уравнение
, неявно задающему общее решение уравнения. Уравнение  называется общим интегралом дифференциального уравнения.
называется общим интегралом дифференциального уравнения.
Определение. Частным решением дифференциального уравнения называется решение, получаемое из общего решения при конкретных значениях произвольных постоянных  .
.
Уравнение  , где
, где  некоторые значения постоянных
некоторые значения постоянных 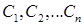 называется частным интегралом дифференциального уравнения.
называется частным интегралом дифференциального уравнения.
21.2.1. Уравнение вида  Решение типовой задачи
Решение типовой задачи
21.2.1.1. Найти общее решение уравнения  .
.
Решение. Этот вид уравнений решается последовательным интегрированием:


 Интегрируя по частям, находим общий интеграл:
Интегрируя по частям, находим общий интеграл: 
21.2.2. Уравнение не содержит переменной  в явном виде. Решение типовых задач
в явном виде. Решение типовых задач
Уравнение вида  Понижение порядка ДУ производится путем замены
Понижение порядка ДУ производится путем замены  .
.
21.2.2.1. Решить уравнение  .
.
Решение. В уравнении отсутствует неизвестная функция  , поэтому порядок уравнения можно понизить путем замены
, поэтому порядок уравнения можно понизить путем замены 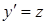 , где
, где  – новая неизвестная функция. Тогда
– новая неизвестная функция. Тогда  и уравнение примет вид
и уравнение примет вид  . Это уравнение с разделяющимися переменными:
. Это уравнение с разделяющимися переменными:

 .
.
Таким образом,  . Подставляя сюда
. Подставляя сюда  , имеем:
, имеем:  . Значит, знак перед корнем должен быть «–», и
. Значит, знак перед корнем должен быть «–», и  . Интегрируем по
. Интегрируем по 
 .
.
Подставим в это равенство  :
:
 – искомое частное решение.
– искомое частное решение.
21.2.2.2. Решить уравнение  ;
;  ,
,  .
.
Решение. Сделаем замену  . Тогда
. Тогда
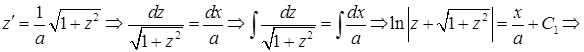
 . Подставляя начальное условие
. Подставляя начальное условие  , получим
, получим
 . Тогда
. Тогда  . Интегрируя уравнение по переменной
. Интегрируя уравнение по переменной  , запишем
, запишем  . С учетом начального условия
. С учетом начального условия  , определяем
, определяем  :
:  . Получим частное решение:
. Получим частное решение:  .
.
21.2.2.3. Найти общее решение уравнения 
Решение. Делаем подстановку 
 или
или  получено линейное уравнение первого порядка. Полагая
получено линейное уравнение первого порядка. Полагая  найдём:
найдём: 








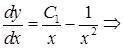
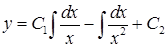 или окончательно
или окончательно 
Задачи для самостоятельного решения
ЧАСТЬ Б)
 2020-06-29
2020-06-29 162
162








