Задача. Докажите, что сложение положительных рациональных чисел ассоциативно.
Решение: Для того чтобы доказать, что для любых положительных рациональных чисел 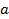 ,
, 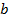 и
и  истинно равенство
истинно равенство  , представим числа
, представим числа 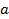 ,
, 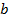 и
и  дробями с одинаковым знаменателем:
дробями с одинаковым знаменателем:
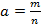 ,
,  ,
, 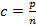 , где
, где 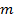 ,
, 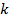 ,
,  и
и  - натуральные числа.
- натуральные числа.
Тогда 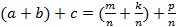 . Воспользуемся правилом сложения дробей с одинаковым знаменателем:
. Воспользуемся правилом сложения дробей с одинаковым знаменателем:
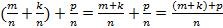 .
.
Т.к. 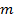 ,
, 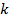 ,
,  - натуральные числа, то на основании ассоциативного закона сложения натуральных чисел получим:
- натуральные числа, то на основании ассоциативного закона сложения натуральных чисел получим:
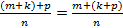 .
.
По правилу сложения дробей имеем:
 , что и требовалось доказать.
, что и требовалось доказать.
Тема 3. Сравнение положительных рациональных чисел
3.1. Расположите дроби в порядке возрастания: 
3.2. Каждую из дробей преобразуйте в несократимую и сравните их: 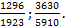
3.3. Запишите по два рациональных числа, заключенных между числами: 
Методические рекомендации
В данной теме предлагаются задачи на сравнение положительных рациональных чисел. Их решение основано на применении практических приемов установления отношения «меньше» («больше») на множестве положительных рациональных чисел:
1. Если a =  , b =
, b =  , то a<b тогда и только тогда, когда m<p;
, то a<b тогда и только тогда, когда m<p;
2. Если a =  , b =
, b =  , то a<b тогда и только тогда, когда mq<np, Для решения задач данной темы необходимо:
, то a<b тогда и только тогда, когда mq<np, Для решения задач данной темы необходимо:
| знать: - определение отношения «меньше» («больше») на множестве положительных рациональных чисел; - практические приемы установления отношения «меньше» («больше») на множестве положительных рациональных чисел; | уметь: - применять практические приемы сравнения положительных рациональных чисел на практике. |
 2020-06-29
2020-06-29 138
138








