2020-06-29
83
Задача 1. а) Представить в виде десятичной дроби числа: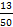 
; 2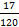 
; 
б) Записать дроби 0,(72); 0,012(27) в виде обыкновенных дробей.
Решение:
а) Каноническое разложение числа 
, значит, 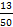может быть записана в виде конечной десятичной дроби с двумя десятичными знаками, т.к. наибольший показатель у 2 и 5 в разложении числа 50 равен 2. Эту дробь получим путем деления числителя на знаменатель. Имеем 
;
Каноническое разложение числа 
, следовательно, число 2 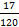может быть записано в виде смешанной периодической бесконечной десятичной дроби 
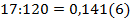; 2 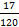= 2,141(6).
Несократимая дробь имеет знаменатель взаимно простой с числом 10, значит, дробь можно записать в виде чистой периодической бесконечной десятичной дроби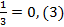 
.
б) Решение: Чтобы чистую периодическую бесконечную десятичную дробь записать в виде обыкновенной, достаточно в числитель записать число, составленное из цифр периода, а в знаменатель число, составленное из 9, причем, их нужно взять столько, сколько цифр в периоде. Итак, 
. Сократим числитель и знаменатель на 9, получим 
.
Чтобы смешанную периодическую бесконечную десятичную дробь записать в виде обыкновенной, достаточно в числитель записать разность между числом, составленном из цифр, стоящих до второго периода, и числом, состоящим из цифр предпериода, а в знаменатель записать число, состоящее из 9, причем их написать столько, сколько цифр в периоде, и 0, а их написать столько, сколько цифр в предпериоде. Итак,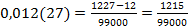 
или, сократив, получим 
.
Тема 5. Действия над десятичными дробями
5.1. Вычислите рациональным способом.
а)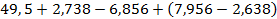 
;
б) 
.
5.2. а) Что больше: 35% от 40 или 40% от 35?
б) Увеличьте число: 60 на 10%; 80 на 2,5%.
5.3. Найдите 10% числа, которое является значением выражения 
.
