Образец выполнения задания

Задача. Какова несократимая запись дробей и 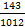? Какая из данных дробей больше?

Решение:

Чтобы получить несократимую запись дроби, необходимо числитель и знаменатель разделить на их наибольший общий делитель. Для дроби  найдем НОД при помощи алгоритма Евклида:

                                                                                   _1242ë351

                                                                                     1053 3

                                                                          _ 351 ë 189

                                                                              189   1

                                                                   _ 189 ë162

                                                                       162 1

                                                           _162 ë27

                                                             162 6

                                                                 0

Итак, (351, 1242)= 27. Разделив 351 и 1242 на 27, получаем несократимую запись дроби .

Аналогично находим НОД (143, 1012)=11. Следовательно,

.

Сравним дроби  и . Их числители равны и потому та дробь больше, у которой знаменатель меньше, т.е. > , а значит > .

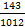Тема 4. Десятичные дроби

4.1. Какие из дробей можно записать в виде конечной десятичной дроби? 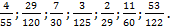  Какие из них преобразуются в чистую, какие в смешанную периодическую бесконечную десятичную дробь? Ответ обоснуйте.

4.2. Следующие числа представьте в виде несократимых обыкновенных дробей: 0,05; 4,0016; 0,(27); 2,32(16); 6,038(72).

4.3. Сравните числа: 3,(4) и 3 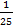; 8,211216 и 8,(211).