Определение: Квадратное неравенство – это неравенство вида:

В случае если a=0, мы получаем линейное неравенство.
Вспомним терминологию.
x - независимая переменная. Необходимо найти множество всех x, при которых неравенство выполняется.
a, b, c – конкретные числа, параметры;
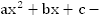 квадратный трехчлен;
квадратный трехчлен;
 квадратичная функция.
квадратичная функция.
Решение квадратного неравенства целиком основано на свойствах квадратичной функции.
Решение квадратного неравенства, когда трехчлен не имеет корней
Например: Решить неравенства:


Рассмотрим функцию  Построим и прочтем ее график.
Построим и прочтем ее график.
Графиком квадратичной функции является парабола, шаблон – парабола  сдвинутая относительно начала координат.
сдвинутая относительно начала координат.
Определим координаты вершины.

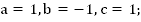

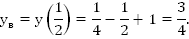
Схематически изобразим график функции. Ветви параболы направлены вверх, т.к. 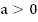 .
.

Теперь прочтем полученный график.
Функция определена при  . Основное свойство данной функции заключается в том, что
. Основное свойство данной функции заключается в том, что  при всех
при всех 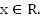 Более того,
Более того, 
Ответ: 

Мы рассмотрели случай, когда график функции не пересекает ось o x.
Решение квадратного неравенства, когда трехчлен имеет один корень
Например: 

Рассмотрим функцию: 
Найдем корни квадратного трехчлена: 
D=8-8=0, значит 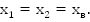
Схематически построим график функции: 
Корень x=1;
графиком является парабола, 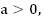 значит ветви направлены вверх.
значит ветви направлены вверх.

Прочитаем график.
На промежутке 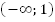 функция положительна. На промежутке
функция положительна. На промежутке 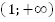 функция также положительна. При
функция также положительна. При 
Ответ: 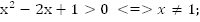

Мы рассмотрели случай, когда кривая касается оси o x в одной точке.
Решение квадратного неравенства, когда трехчлен имеет два корня
Например:

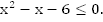
Найдем корни квадратного трехчлена:  Воспользуемся теоремой Виета.
Воспользуемся теоремой Виета.
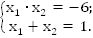
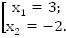
Схематически изобразим график функции: 
Это парабола, ветви направлены вверх, т.к. 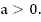

Прочитаем график. На промежутке  функция положительна.
функция положительна.
На промежутке 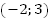 функция отрицательна.
функция отрицательна.
В точках пересечения с осью O x функция равна нулю.
Ответ: 
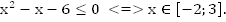
 2020-06-29
2020-06-29 86
86








