2020-06-29
85
Уважаемые студенты,
Переходим к изучению непрерывных случайных величин.
Вам на сайте http://mathprofi.ru/nepreryvnaya_sluchaynaya_velichina.html
(можно читать не всё) и (или) по Приложению 1 надо изучить понятия:
- непрерывная случайная величина (НСВ)
- функция распределения НСВ (интегральная функция распределения)
- плотность вероятности НСВ (дифференциальная функция распределения)
- числовые характеристики НСВ (математическое ожидание, дисперсия,
среднее квадратичное отклонение)
Научиться вычислять вероятность попадания НСВ в некоторый промежуток.
После изучения теории надо выполнить практическую работу.
Обратите внимание на необходимость вспомнить дифференцирование и интегрирование функций (в заданиях только табличные интегралы!).
Примеры решения задач и построения графиков смотреть на сайте.
Вариант № 1
1.Случайная величина задана функцией распределения  .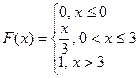
a). Найти плотность вероятности f (x).
b) Найти математическое ожидание и дисперсию случайной величины.
c) Построить графики плотности вероятности и функции распределения.
d) Найти вероятность того, что случайная величина примет значение
из промежутка (1; 2).
2.Случайная величина задана плотностью вероятности  .
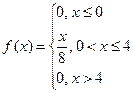a) Найти математическое ожидание и дисперсию случайной величины.
b) Найти функцию распределения вероятности.
c) Построить графики плотности вероятности и функции распределения.
d) Найти вероятность того, что случайная величина примет значение
из промежутка (3; 3,5).
|
Вариант № 2
1.Случайная величина задана функцией распределения  .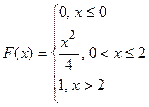
a) Найти плотность вероятности f (x).
b) Найти математическое ожидание и дисперсию случайной величины.
c) Построить графики плотности вероятности и функции распределения.
d) Найти вероятность того, что случайная величина примет значение из промежутка (1; 1,5).
2. Случайная величина задана плотностью вероятности  .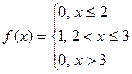
а) Найти математическое ожидание и дисперсию случайной величины.
b) Найти функцию распределения вероятности.
с) Построить графики плотности вероятности и функции распределения.
д) Найти вероятность того, что случайная величина примет значение из промежутка (2,1; 2,5).
|
Вариант № 3
1.Случайная величина задана функцией распределения  .
a) Найти плотность вероятности f (x).
b) Найти математическое ожидание и дисперсию случайной величины.
c) Построить графики плотности вероятности и функции распределения.
d) Найти вероятность того, что случайная величина примет значение из промежутка (0,5; 1).
2.Случайная величина задана плотностью вероятности  .
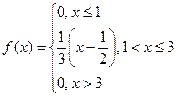a) Найти математическое ожидание и дисперсию случайной величины.
b) Найти функцию распределения вероятности.
c) Построить графики плотности вероятности и функции распределения.
d) Найти вероятность того, что случайная величина примет значение
из промежутка (1,5; 3,5).
|
Вариант № 4
1.Функция распределения непрерывной случайной величины F(x) равна 0, если x £ 0, вычисляется по формуле 2 x, если 0 < x £ 0,5, принимает значение 1, если x > 0,5.
а) Найти плотность вероятности f (x)
в) Найти математическое ожидание и дисперсию случайной величины.
с) Построить графики плотности вероятности и функции распределения.
д) Найти вероятность того, что случайная величина примет значение из промежутка (0,1; 0,5).
2.Случайная величина задана плотностью вероятности  .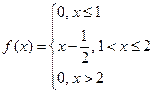
a) Найти математическое ожидание и дисперсию случайной величины.
b) Найти функцию распределения вероятности.
c) Построить графики плотности вероятности и функции распределения.
d) Найти вероятность того, что случайная величина примет значение
из промежутка (1,5; +∞).
|
Распределение вариантов:
| Вариант | Фамилии студентов |
| 1 | Баталов, Кравцова, Синявская, Рудник, Ошурков, Черноусов, Пономарёв И., |
| 2 | Лукина, Изибаев, Саулич, Жигаляк, Трясцин, Касьянов, Никитин,, Отраднов, Третьяков |
| 3 | Колташев, Пономарев Н., Степанов, Паньшин, Юксеев, Синкин, Чухарев, Перминов |
| 4 | Игнатов, Нусс, Подрядов, Поросёнков, Армянинова, Генова Колбич, Желудков |
Файлы (фото записей в тетрадях) присылать до 16.05 на почту tdpatrakova@mail.ru
Приложение 1.
