Теорема о площади боковой поверхности правильной пирамиды

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему:

Для доказательства выберем правильную треугольную пирамиду.

Дано: РАВС – правильная треугольная пирамида.

АВ = ВС = АС.

РО – высота.

Доказать: . См. Рис. 5.

Рис. 5

Доказательство.

РАВС – правильная треугольная пирамида. То есть АВ = АС = ВС. Пусть О – центр треугольника АВС, тогда РО – это высота пирамиды. В основании пирамиды лежит равносторонний треугольник АВС. Заметим, что .

Треугольники РАВ, РВC, РСА – равные равнобедренные треугольники (по свойству). У треугольной пирамиды три боковые грани: РАВ, РВC, РСА. Значит, площадь боковой поверхности пирамиды равна:

S_бок = 3S_РАВ

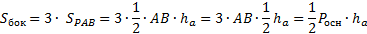
Теорема доказана.

Задача 1

Радиус окружности, вписанной в основание правильной четырехугольной пирамиды, равен 3 м, высота пирамиды равна 4 м. Найдите площадь боковой поверхности пирамиды.

Дано: правильная четырехугольная пирамида АВСD,

АВСD – квадрат,

r = 3 м,

РО – высота пирамиды,

РО = 4 м.

Найти: S_бок. См. Рис. 6.

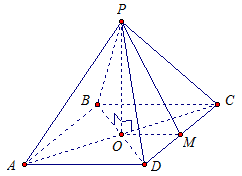
Рис. 6

Решение.

По доказанной теореме, .

Найдем сначала сторону основания АВ. Нам известно, что радиус окружности, вписанной в основание правильной четырехугольной пирамиды, равен 3 м.

Тогда, 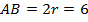м.

Найдем периметр квадрата АВСD со стороной 6 м:

Рассмотрим треугольник BCD. Пусть М – середина стороны DC. Так как О – середина BD, то (м).

Треугольник DPC – равнобедренный. М – середина DC. То есть, РМ – медиана, а значит, и высота в треугольнике DPC. Тогда РМ – апофема пирамиды.

РО – высота пирамиды. Тогда, прямая РО перпендикулярна плоскости АВС, а значит, и прямой ОМ, лежащей в ней. Найдем апофему РМ из прямоугольного треугольника РОМ.

(м).

Теперь можем найти боковую поверхность пирамиды:

Ответ: 60 м²_.

 Решите задачу № 1207 стр. 316