Определение комплексных чисел. Алгебраическая форма комплексного числа

Комплексным числом называется выражение а+bi, где а, b – действительные числа, а і – некий символ.

Множество комплексных чисел обозначается буквой С.

Запись комплексного числа в виде:

z=а+bi   (1)

называют алгебраической формой комплексного числа. Причем а – действительная часть комплексного числа Re(z), а bi –   мнимая часть комплексного числа Im(z).

Два комплексных числа считаются равными, если они имеют равные действительные и мнимые части.

В комплексном числе мнимая единица і определяется равенством: і² = -1.

Любое действительное число можно записать в виде комплексного числа:

z=а+0i.

если а = 0, то комплексное число становится чисто мнимым z =bi.

Два комплексных числа вида: z=а+bi и z =а-bi называются комплексно сопряженными.

Условились комплексное число z=а+bi отображать точкой плоскости с координатами (а;b). Действительные числа изображаются точками оси абсцисс, которую называют действительной осью, а чисто мнимые числа – точками оси ординат, которую называют мнимой осью. Каждому комплексному числу z=а+bi соответствует точка на плоскости с координатами (а;b), или радиус вектор, начало которого лежит в начале координат, а конец в точке (а;b).

Модулем комплексного числа называется длина соответствующего ему вектора. Модуль комплексного числа z  обозначается ІzІ и часто модуль обозначают буквой r.

Значение модуля вычисляют по теореме Пифагора по формуле:

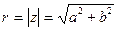.   (2)

Если модуль равен некоторому положительному числу, то по определению модуля имеют место утверждения:

- множество всех чисел: z, для которых ІzІ= r, является окружностью с радиусом r и центром в начале координат;

- множество всех чисел: z, для которых ІzІ≤ r, является круг с радиусом r і центром в начале координат;

- множество всех чисел: z, для которых ІzІ › r, является дополнение (внешние точки) окружности радиусом r и центром в начале координат.

 

3.. Действия над комплексными числами в алгебраической форме

Пусть заданы комплексные числа:      и      

Суммой чисел      и        называется число:

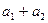+ =()+() і         (3)

 Произведением чисел      и        называется число:

(4)

Частным чисел      и        называется число:

                (5)

Для комплексных чисел выполняется коммутативный и ассоциативный закон для сложения, а также коммутативный, ассоциативный и дистрибутивный законы для умножения.

Приведем примеры решения упражнений:

1) найти сумму и произведение комплексных чисел 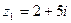 и .

Решение:

+ =(2-1)+(5+7)і=1+12і;

=(2+5і)(-1+7і)=-2+14і-5і+35і²=-2+9і-35=-37+9і;

 

2) решить уравнение:

х²-4х+13=0.

Решение:

D=16-52=-36, заменим -1 на і², тогда: .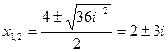

 

3) найти частное комплексных чисел  та

Решение:

 

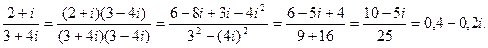
4) вычислить: і³

Решение:

і³= і²∙і = (-1)∙і =-і.

Задания для закрепления и самоконтроля:

1) Решить уравнение: 5х²+6х+5=0. Ответ:  .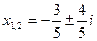

2) Вычислить сумму, разность, произведение комплексных чисел:

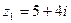 та .                    Ответ: 3+7і; 7+і; -22+7і;

3) Вычислить 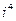.                              Ответ:1.

4) Найти частное комплексных чисел: (-1+6і); (2+5і).

Ответ: 28/37 – 17/37 і.

5) Изобразить комплексные числа в системе координат и показать их суммарный вектор: (-2+і); (3+3і).

Контрольные вопросы.

1. Что называется комплексным числом?

2. Какие существуют формы записи комплексных чисел?

3. Что называют мнимой единицей?

4. Какие действия можно выполнять над комплексными числами, заданными   в алгебраической форме?

5. Чем отличается действительная часть комплексного числа от мнимой?

6. Как изобразить комплексное число на плоскости?

7. Дать геометрическую интерпретацию суммы и разности комплексных чисел.

8. Изобразить на плоскости комплексные числа: -2і; 6+3і; 4; -3-5і; 2-і.

9. Как найти сумму двух комплексных чисел?

10. Как вычислить произведение комплексных чисел?

11. Какие числа называются комплексно-сопряженными?

12. Как вычислить частное комплексных чисел?

13. Как решить квадратное уравнение с отрицательным дискриминантом?

Литература:

И.И..Валуцэ, Г.Д.Дилигул «Математика для техникумов», М.,1989, ст.78-95.

 

ЛЕКЦИЯ № 15

 

Модуль 2. Комплексные числа.

 

Тема: Тригонометрическая форма комплексного числа.

Цели: ознакомить с понятием аргумента комплексного числа, рассмотреть правила действий над комплексными числами в тригонометрической форме.

План.

1. Аргумент комплексного числа.

2. Тригонометрическая форма комплексного числа.

3. Действия над комплексными числами в тригонометрической форме