Коэффициент полезного действия источника тока

Исследуем физические характеристики замкнутой электрической цепи, включающей внешнее сопротивление, называемое полезной нагрузкой, и источник тока с электродвижущей силой и внутренним сопротивлением (рис. 3).При прохождении тока тепло выделяется как на внешнем, так и внутреннем сопротивлении. Полная тепловая мощность 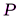, выделяемая в цепи постоянного тока, складывается из полезной мощности

,                                                            (6.17)

выделяемой во внешней цепи, и мощности тепловых потерь , выделяемой внутри источника тока, т.е.

.                                     (6.18)

Рис. 6. 3

Полная мощность развивается за счет сторонних сил, осуществляющих разделение зарядов в источнике тока. Используя закон Ома для замкнутой цепи [см. формулу (6.13)], выражения для полезной и полной тепловых мощностей можно записать в виде

                                            (6.19)

и

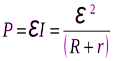.                                (6.20)

Коэффициент полезного действия (КПД) электрической цепи определяется как отношение полезной мощности к полной мощности:

.                                        (6.21)

Таким образом, КПД зависит от соотношения внутреннего сопротивления и сопротивления нагрузки.

Каким должно быть сопротивление нагрузки для того, чтобы получить максимальную полезную мощность и максимальный КПД? Ответ на этот вопрос получим, исследовав графически и аналитически выражения (6.19) и (6.21).

Полная мощность определяется формулой (12). Ее величина максимальна при , т.е. при коротком замыкании источника. Как видно из формул (11) и (13), при этом равны нулю Р_п и (рис. 6.4.).

При полная мощность и сила тока равны половинам своих максимальных значений, КПД равен 0,5, а полезная мощность достигает своего максимального значения, равного половине полной мощности при этой нагрузке.

Чтобы убедиться, что при равенстве сопротивления нагрузки и внутреннего сопротивления источника тока полезная мощность действительно максимальна, преобразуем правую часть выражения (6.19) следующим образом:

.                                        (6.22)

Рис. 6.4.

Полезная мощность максимальна, когда знаменатель выражения (6.22) минимален. Возьмем производную по R от этого знаменателя и приравняем ее нулю. В результате получим уравнение

,                                                    (6.23)

из которого следует, что условием максимума полезной мощности действительно является равенство внешнего и внутреннего сопротивлений.

Сам максимум полезной мощности определяется как

,                                           (6.24)

то есть максимум полезной мощности равен четверти мощности короткого замыкания:

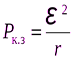.                                              (6.25)

При неограниченном увеличении сопротивления нагрузки как полная мощность, так и полезная мощность стремятся к нулю, а КПД – к единице (рис.6.4).

Из рис. 6.4 видно, что требования получения максимального тока в цепи, максимальной полезной мощности и максимального КПД противоречивы. Для получения возможно большего тока сопротивление нагрузки должно быть малым по сравнению с внутренним сопротивлением источника, но при этом близки к нулю полезная мощность и КПД, так как почти вся совершаемая источником тока работа идет на выделение теплоты на внутреннем сопротивлении r. Чтобы получить от данного источника тока максимальную полезную мощность, следует использовать согласованную нагрузку, т.е. нагрузку с сопротивлением .