2020-06-29
93
Напомним некоторые сведения о системе неравенств. Итак, пусть нам надо найти все значения переменной икс, которые являются решениями каждого из неравенств 
и 
.
Говорят, что надо решить систему неравенств:
Записанная система неравенств является примером системы из двух линейных неравенств с одной переменной (с одним неизвестным).
Значения переменной, которые являются решениями каждого неравенства системы, называются решениями системы. Решить систему неравенств – это значит найти все её решения или доказать, что их нет.
Две системы неравенств называются равносильными, если каждое решение первой системы является решением второй системы, и наоборот – каждое решение второй системы является решением первой системы, то есть если они имеют одни и те же решения. Равносильными называются и системы, которые не имеют решений.
Мы с вами повторили основные моменты, а теперь давайте перейдём к практической части занятия.
Задание первое. Решите системы неравенств:
а) 
б) 
в) 
г) 
Решение.
Задание второе. Решите системы неравенств:
а) 
б)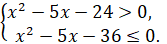 
Решение.
Задание третье. Решите систему неравенств: 
.
Решение.
Задание четвёртое. Решите систему неравенств: 
.
Решение.
