2020-06-29
108
Напомним, что неравенство, содержащее одну переменную, называется неравенством с одной переменной, или неравенством с одной неизвестной.
, 
, , 
, 
,
где 
, 
– некоторые функции переменной 
.
Неравенства, содержащие знаки 
или 
, называются строгими, а содержащие знаки 
или 
– нестрогими.
Решением неравенства с одной переменной называется такое значение переменной, при подстановке которого неравенство обращается в верное числовое неравенство. Решить неравенство – это значит найти все его решения или доказать, что решений нет.
Равносильными называются неравенства, множества решений которых совпадают. В частности, равносильны все неравенства, не имеющие корней.
Теоремы о равносильности неравенств с переменными.
1. 
.
2. 
, если 
имеет смысл
в области определения неравенства .
3. 
, если 
для всех значений из области определения неравенства .
4. 
, если 
для всех значений из области определения неравенства .
5. 
.
6. 
если , 
; 
.
Напомним, что линейным неравенством называется неравенство вида
(
, 
, 
),
где – переменная, 
и 
.
Давайте решим следующее неравенство: 
.
Решение.
Теперь вспомним, что квадратным неравенством называется неравенство вида
(
, 
, 
),
где – переменная, 
, 
, 
, причём 
.
Существует два метода решения квадратных неравенств. Первый метод – графический. При решении неравенств этим методом определяется одно из шести возможных расположений графика в зависимости от знаков старшего коэффициента и 
.
Так, например, если рассматривать неравенство , то из приведённой таблицы видно, что 
, если 
, 
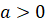. Решением будет 
, если , 
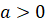. Неравенство не имеет решений, если ,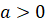 
. Решением является 
если 
, . Решением неравенства будет 
, если , и , .
Давайте решим квадратное неравенство графическим методом: 
.
Решение.
Рассмотрим аналитический метод решения неравенств. Его также называют методом интервалов. Так, например, при решении неравенства этим методом сначала находятся корни квадратного трёхчлена, и он раскладывается на множители 
.
Если 
, то неравенство равносильно неравенству 
.
Если 
, то неравенство равносильно 
.
Затем полученные неравенства можно решить методом интервалов. При решении неравенств метод интервалов нужно:
1. найти нули функции, заданной левой частью неравенства;
2. нанести найденные точки на числовую прямую, тем самым разбив её на интервалы, в каждом из которых рациональная функция сохраняет знак (причём если мы решаем строгое неравенство, то точки изображаем выколотыми, а если решаем нестрогое неравенство, то закрашенными);
3. определить знак функции на любом из интервалов (лучше крайнем);
4. определить знаки на остальных интервалах: при переходе через точку знак меняется на противоположный, если точка является корнем нечётной степени кратности; при переходе через точку чётной кратности знак сохраняется;
5. затем выбрать интервалы, на которых значения функции имеют знак, соответствующий знаку неравенства;
6. записать ответ.
Решим методом интервалов предыдущее неравенство: .
Решение.
Теперь вспомним, что рациональным неравенством называется неравенство, которое содержит только рациональные функции.
Например, 
; 
– рациональные неравенства.
Линейные и квадратные неравенства также являются рациональными.
Рациональные неравенства бывают целыми (в них нет операции деления на выражение, содержащее переменную).
Например, 
.
И бывают дробно-рациональными (в них есть операция деления на выражение, содержащее переменную).
Например, 
.
Основным методом решения рациональных неравенств является метод интервалов.
Давайте решим следующее неравенство: 
.
Решение.
Также напомним, что иррациональным неравенством называется неравенство, которое содержит переменные под знаком корня. Основным методом решения иррациональных неравенств является метод сведения исходного неравенства к равносильной системе рациональных неравенств или совокупности таких систем.
Решим следующее неравенство: 
.
Решение.
