Знайдемо струм 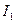 методом еквівалентного генератора. Згідно з цим струм
методом еквівалентного генератора. Згідно з цим струм 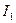 дорівнює:
дорівнює:
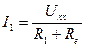 .
.
 |
Для того, щоб знайти параметри еквівалентного генератора
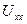 та
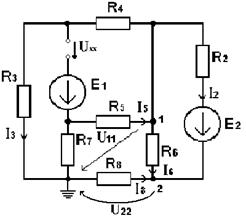
та 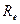 розриваємо гілку 1 так, щоб зберегти джерело енергії в ній (мал. 5).
розриваємо гілку 1 так, щоб зберегти джерело енергії в ній (мал. 5).
Мал. 5. Схема для методу еквівалентного генератора
Після розриву гілки 1 схема спрощується: резистори 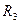 та
та 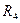 тепер утворюють одну гілку із струмом
тепер утворюють одну гілку із струмом 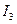 , а резистори
, а резистори 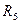 та
та 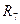 – одну гілку із загальним струмом
– одну гілку із загальним струмом 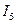 .
.
Розрахуємо напругу холостого ходу, склавши рівняння другого закону Кирхгофа:
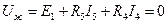 .
.
Для того, щоб розрахувати 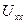 , необхідно знати струми
, необхідно знати струми 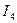 та
та 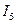
Після розриву 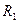 схема містить три незалежні контури і два незалежні вузли. Тому розрахуємо струми методом вузлової напруги. Система рівнянь в загальному вигляді буде такою:
схема містить три незалежні контури і два незалежні вузли. Тому розрахуємо струми методом вузлової напруги. Система рівнянь в загальному вигляді буде такою:
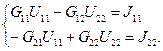
Власні провідності вузлів:
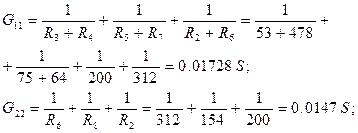
Загальна провідність вузлів:
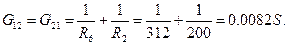
Вузлові струми:

Система має вигляд:
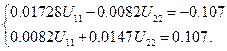
Її розв’язання: 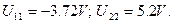
Знаючи вузлові напруги, розрахуємо потрібні нам струми і:
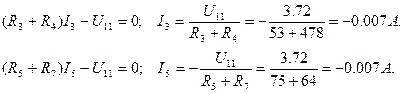
Тепер можна знайти:
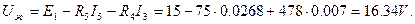
Для розрахунку 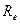 виключимо з схеми джерела енергії, залишивши їх внутрішні опори. Для цього наявні в схемі джерела напруги необхідно замкнути. Схема без джерел має вигляд, показаний на мал. 6:
виключимо з схеми джерела енергії, залишивши їх внутрішні опори. Для цього наявні в схемі джерела напруги необхідно замкнути. Схема без джерел має вигляд, показаний на мал. 6:
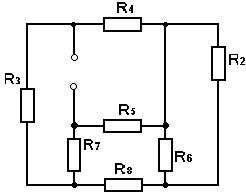
Мал. 6. Схема для визначення 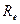
В схемі на мал. 6 резистори 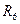 та
та 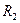 з’єднані паралельно, а резистор
з’єднані паралельно, а резистор 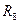 – з ними послідовно. Опір еквівалентного резистору
– з ними послідовно. Опір еквівалентного резистору 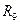 дорівнюватиме:
дорівнюватиме:
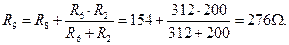
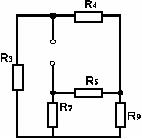 |
З урахуванням цієї заміни маємо схему, що показана на рис. 7.
Мал. 7. Схема після заміни послідовного та паралельного з’єднань
В ній резистори 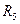 ,
, 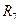 и
и 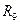 з’єднані трикутником. Замінимо таке з’єднання еквівалентною зіркою
з’єднані трикутником. Замінимо таке з’єднання еквівалентною зіркою 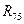 ,
, 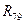 ,
, 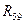 . Маємо:
. Маємо:
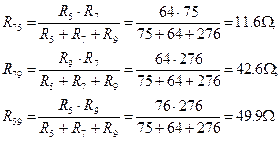
Після заміни схема має вигляд (мал. 8):
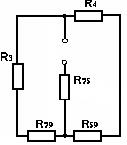 |
Мал. 8. Схема після заміни трикутника зіркою
У цій схемі резистори 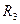 та
та 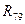 , а також
, а також 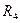 та
та 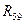 сполучені послідовно, а гілки, що містять ці резистори сполучені паралельно. Еквівалентне паралельне з'єднання гілок підключене послідовно з
сполучені послідовно, а гілки, що містять ці резистори сполучені паралельно. Еквівалентне паралельне з'єднання гілок підключене послідовно з 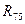 . Тому еквівалентний опір генератора можна знайти як:
. Тому еквівалентний опір генератора можна знайти як:
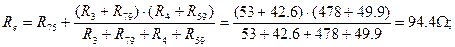
Тепер можна визначити по формулі еквівалентного генератора струм в гілці 1: 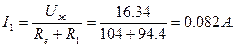
Цей струм збігається із знайденим раніше, що свідчить про правильність обчислень.
 2020-06-30
2020-06-30 146
146








