Линейные операции над матрицами

2 3 4 5 6 7 8

Умножение матрицы A на число k:

B = k × A = ,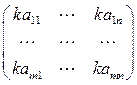

или, в краткой записи:

B = k × A Û b_ij = k × a_ij (i = 1,2,…, m; j = 1,2,…, n) . (19)

Сложение (вычитание) матриц A и B одинаковой размерности:

C_m_´_n = A_m_´_n ± B_m_´_n Û c_ij = a_ij ± b_ij (i = 1,2,…, m; j = 1,2,…, n). (20)

Произведение матриц A_m_´_n и B_n_´_k:

C_m_´_k = A_m_´_n × B_n_´_k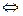

c_ij= a_i1b_1j+ a_i2b_2j+ ¼ + a_inb_nj (i = 1,2,…, m; j = 1,2,…, k). (21)

Формулу (21) легко запомнить, как правило умножения «строка на столбец»: произведение матриц A_m_´_n и B_n_´_k есть матрица C_m_´_k, у которой элемент c_ij равен сумме произведений соответствующих элементов i- й строки матрицы A и j- го столбца матрицы В.

Замечание. Перемножать можно только соответственные матрицы А и В, т.е.число столбцов матрицы А должно быть равно числу строк матрицы В.

Если задан многочлен 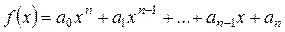, то матричным многочленом 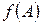называется выражение

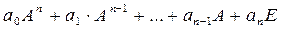где А – квадратная матрица, 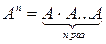и Е – единичная матрица той же размерности, что и А. Значением матричного многочлена является матрица.

Определители

Определитель второго порядка (определитель квадратной матрицы второго порядка):

det A = 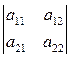= a ₁₁ a ₂₂– a ₁₂ a ₂₁. (22)

Определитель третьего порядка (определитель квадратной матрицы третьего порядка):

det A = (23)

Для краткости определитель обозначают: | A | или Δ.

Минором элемента a_ij определителя называется определитель, которыйполучается из исходного путем вычеркивания i -й строки и j -го столбца (обозначается M_ij).

Алгебраическим дополнением элемента a_ij определителя (обозначается A_ij) называется число:

A_ij = (–1) ⁱ⁺^j× M_ij. (24)

Определитель третьего порядка можно вычислить, используя его разложение по 1-й строке:

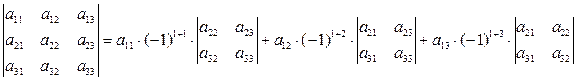, (25)

или, в краткой записи:

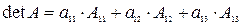т.е. определитель равен сумме произведений элементов первой строки на их алгебраические дополнения. Аналогично можно записать разложение определителя по любой другой строке или столбцу.

4. Решение системы трех линейных алгебраических уравнений с тремя неизвестными методом Крамера

Пусть дана система трех линейных алгебраическихуравнений с тремя неизвестными :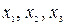

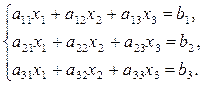(26)

(коэффициенты a_ij и свободные члены b_j для i = 1, 2, 3, j = 1, 2, 3 считаются заданными).

Тройка чисел 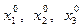называется решением системы (26), если в результате подстановки этих чисел вместо 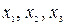все три уравнения системы обращаются в тождества.

Систему (26) можно переписать в матричном виде:

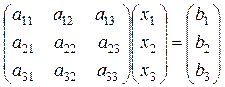, или AX = B,

где A – это матрица коэффициентов при неизвестных, Х – столбец неизвестных, В – столбец свободных членов:

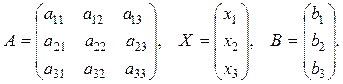
Составим определитель матрицы А и три вспомогательных определителя:

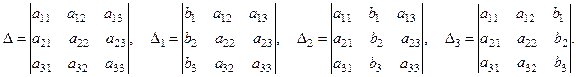(27)

Определитель Δ называется главным определителем системы (26). Вспомогательные определители Δ₁, Δ₂ и Δ₃ получаются из Δ заменой элементов соответственно первого, второго и третьего столбцов столбцом свободных членов.

Если определитель 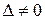, то существует единственное решение системы (26) и оно выражается формулами:

(28)

Формулы (28) называются формулами Крамера.

5. Решение системы трех линейных алгебраических уравнений при помощи обратной матрицы

Присоединенной (союзной) матрицей к квадратной матрице

А= 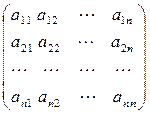называется матрица

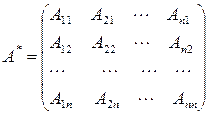, (29)

где – алгебраические дополнения элементов 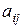определителя матрицы А.

Матрица 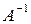называется обратной к квадратной матрице А, если выполнено условие: 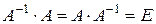, где Е – единичная матрица той же размерности, что и А.

Обратная матрица существует тогда и только тогда, когда квадратная матрица А – невырожденная, т.е. .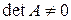

Чтобы найти обратную матрицу 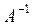, необходимо:

а) проверить невырожденность матрицы А, вычислив определитель det A;

б) найти союзную матрицу А ^* к матрице А;

в) найти обратную матрицу по формуле:

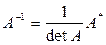. (30)

Если систему линейных алгебраических уравнений(26) переписать в матричном виде AX = B, то ее решение можно получить матричным способом, т.е. при помощи обратной матрицы:

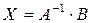, (31)

где 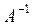– обратная матрица для данной матрицы А.

6. Векторы. Операции над векторами

Вектор 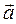может быть представлен в виде:

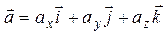(32)

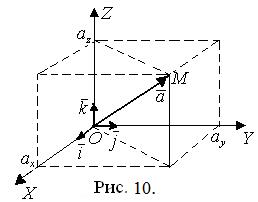где 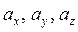– проекции вектора 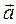на оси координат (координаты вектора), векторы 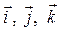– это орты (единичные векторы) координатных осей (рис. 10).

Векторную формулу (32) можно писать сокращенно: 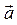= { a_x; a_y; a_z }.

Орты 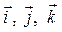имеют проекции:

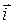={1; 0; 0}, 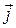={0; 1; 0}, 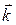={0; 0; 1}.

Модуль (длина) вектора 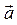= { a_x; a_y; a_z } определяется по формуле:

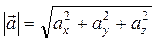. (33)

Координатами точки М называют проекции ее радиус-вектора 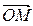(рис. 10). Обозначают координаты точки М (x; y; x) или М (x_М; y_М; x_М).

Расстояние между точками А (x_А, y_А, z_А) и B (x_В, y_B, z_B,) определяется по формуле:

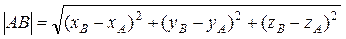. (34)

Если известны координаты точек – начала и конца вектора :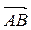

А (x_А, y_А, z_А), B (x_В, y_B, z_B), то проекции вектора 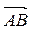можно найти по формуле:

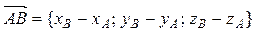. (35)

Пусть даны векторы 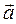= { a_x; a_y; a_z } и 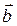= { b_x; b_y; b_z }, тогда проекции суммы (разности) векторов:

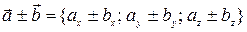. (36)

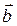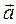Произведение вектора на число: если λ – число и = λ , то

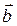= { λa_x; λa_y; λa_z }. (37)

Скалярное произведение векторов и 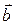– это число, равное произведению модулей векторов на косинус угла между ними:

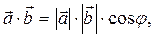
где φ – угол между векторами и .

Другие обозначения скалярного произведения: , .

Если = { a_x; a_y; a_z }, 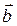= { b_x; b_y; b_z }, то скалярное произведение

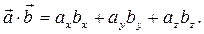(38)

При помощи скалярного произведения можно найти угол между векторами:

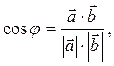(39)

а также проекцию одного вектора на ось другого вектора:

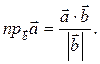(40)

Векторное произведение вектора 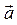на вектор 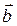– это вектор 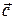, удовлетворяющий трем условиям:

1) , ;

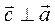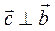2) векторы 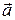, 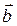и 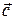образую правую тройку;

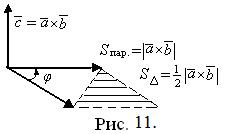
3) 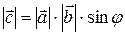, то есть | 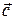| равен площади параллелограмма, построенного на векторах 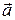и 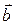(рис. 11).

Обозначения векторного произведения: , .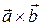

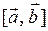Если 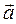= { a_x; a_y; a_z }, 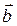= { b_x; b_y; b_z }, то векторное произведение можно вычислить при помощи определителя: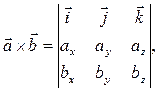

или, с использованием формулы (25):

(41)

Векторное произведение используют, когда нужно найти вектор 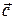, перпендикулярный двум данным векторам 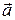и 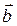: 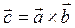, а также для вычисления площади параллелограмма (или треугольника), построенного на векторах 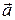и 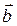(рис. 11):

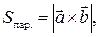
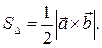(42)

Смешанным произведением трех векторов 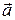, 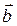и 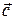называется число, равное скалярному произведению векторов 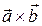и .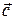

Обозначения смешанного произведения: 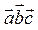или .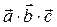

Если 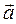= { a_x; a_y; a_z }, 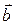= { b_x; b_y; b_z } и 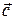= { с_x; с_y; с_z }, то смешанное произведение можно вычислить при помощи определителя:

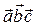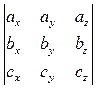= . (43)

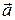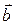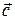Если три ненулевых вектора , и параллельны одной и той же плоскости (компланарны), то их смешанное произведение равно нулю:

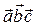= 0. (44)

Объем V параллелепипеда, построенного на векторах 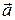, 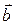и можно вычислить по формуле:

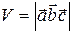. (45)

7. Уравнение плоскости в пространстве

Общее уравнение плоскости: ,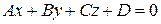

где A, B, C – координаты вектора нормали вектора 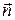(любого вектора, перпендикулярного данной плоскости), D – свободный член уравнения.

Уравнение плоскости, проходящей через точку 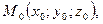перпендикулярно вектору :

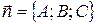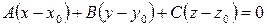. (46)

Уравнение плоскости, проходящей через три заданные точки :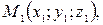

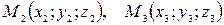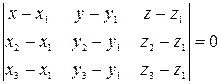. (47)

Угол 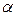между двумя плоскостями, заданными уравнениям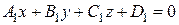и и 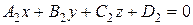определяется как угол между векторами их нормале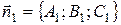й и 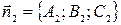или дополнительный к нему (обычно берется острый угол), то есть

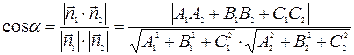. (48)

8. Уравнения прямой в пространстве

Параметрические уравнения прямой l в пространстве:

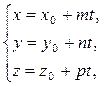(49)

где 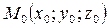– фиксированная точка прямой;

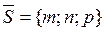– направляющий вектор прямой l, т.е. любой вектор, параллельный l;

t – числовой параметр.

Каждому значению параметра 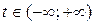соответствует единственная точка прямой l.

Канонические уравнения прямой:

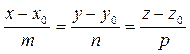. (50)

Уравнения прямой, проходящей через две данные точк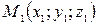и и :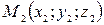

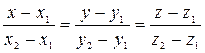. (51)

Углом между прямыми называют угол между их направляющими векторами ={ m ₁; n ₁; p ₁} и ={ m ₂; n ₂; p ₂}, или дополнительный к нему (обычно берется острый угол), то есть

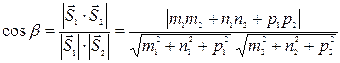. (52)

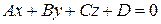Углом между плоскостью и прямой l (в случае их пересечения) называется угол между прямой и её проекцией на плоскость. Синус угла между плоскостью и прямой 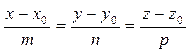определяется по формуле: