Варианты контрольной работы

Задача 1. Даны координаты вершин треугольника АВС.

 

№ варианта	Координаты точек	№ варианта	Координаты точек
1	А (–2; –3), В (2; 7), С (6; –1)	6	А (3; –3), В (–4; 1), С (–2; 5)
2	А (–5; 1), В (6; 3), С (–4; –7)	7	А (3; 5), В (–2; 2), С (2; –4)
3	А (4; 5), В (–3; 2), С (5; –4)	8	А (–2; 4), В (5; 6), С (3; –4)
4	А (7; –7), В (1; 2), С (–5; –4)	9	А (3; 7), В (–4; 1), С (–2; –5)
5	А (–3; 4), В (4; 5), С (8; –3)	10	А (4; 3), В (–3; –2), С (–7; 2)

 

Требуется:

1) вычислить длину стороны ВС; 

2) составить уравнение стороны ВС; 

3) найти внутренний угол треугольника при вершине В; 

4) составить уравнение высоты АК, проведенной из вершины А;  

5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан);

6) сделать чертеж в системе координат.

 

 

Задача 2. Дано уравнение кривой 2-го порядка.

 

№ вар.	Уравнение кривой	№ вар.	Уравнение кривой
1	7 x 2 – 9 y 2  + 42 x+ 18 y – 9= 0	6	9 x 2 + 4 y 2  – 54 x+ 8 y+ 49= 0
2	x 2 + 2 x – 12 y + 37= 0	7	x 2 – 10 x + 4 y + 17= 0
3	5 x 2 + 9 y 2  + 10 x – 54 y + 41= 0	8	3 x 2 – y 2  – 30 x – 2 y + 62= 0
4	y 2  + 6 x+ 6 y – 3= 0	9	y 2  – 8 x – 4 y – 4= 0
5	5 x 2 – 4 y 2  – 20 x – 24 y – 36= 0	10	7 x 2 + 16 y 2  – 56 x+ 64 y+ 64= 0

 

Привести заданное уравнение к каноническому виду путем параллельного переноса осей координат. Определить тип кривой, найти ее характерные элементы в исходной системе координат. Изобразить на чертеже расположение кривой относительно обеих систем координат.

Задача 3. Даны уравнение кривой 2-го порядка и уравнение прямой.

 

№ варианта	Уравнение кривой	Уравнение прямой
1	x 2 + 2 y 2  – 2 x + 8 y + 3= 0	x  + 2 y + 3= 0
2	x 2 – 2 y 2  + 4 x + 4 y – 6= 0	x + 2 y = 0
3	x 2 + 6 x – 16 y + 25= 0	x – 4 y + 15= 0
4	x 2 + 4 y 2  – 6 x + 8 y + 5= 0	x – 2 y – 5= 0
5	y 2  – 4 x – 6 y – 15= 0	2 x + y – 3= 0
6	x 2 – 5 y 2  + 10 x + 20 y – 15= 0	x – 5 y + 15= 0
7	x 2 + 4 y 2  + 2 x – 32 y + 45= 0	x – y + 5= 0
8	x 2 – 4 x + 8 y + 44= 0	x – 2 y – 20= 0
9	2 x 2 – y 2  – 16 x – 6 y + 19= 0	x – y – 7= 0
10	y 2  + 10 x + 8 y – 34= 0	2 x + y + 4= 0

 

Требуется:  

1) привести заданное уравнение кривой 2-го порядка к каноническому виду; 2) найти точки пересечения кривой и заданной прямой; 

3) построить обе линии в исходной системе координат.

 

Задача 4. Даны многочлен   f (x) и матрица А.

 

№ варианта	многочлен   f (x)	Матрица   А
1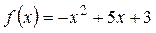
2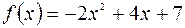
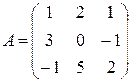
3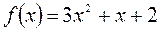
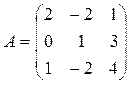
4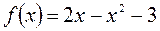
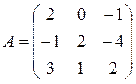
5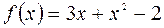
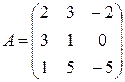
6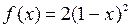
7
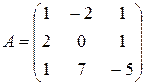
8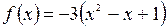
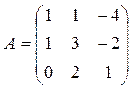
9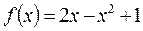
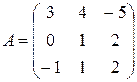
10

 

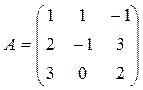
Требуется найти значение матричного многочлена .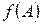

Задача 5. Дана система трех линейных алгебраических уравнений с тремя неизвестными.

№ варианта	Система уравнений	№ варианта	Система уравнений
1		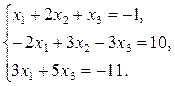6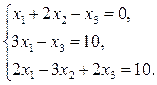
2		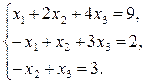7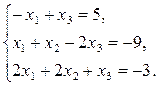
3		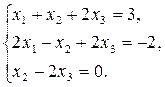8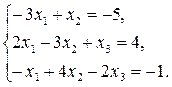
4		9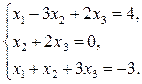
5		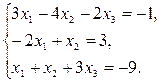10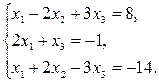

Требуется:

1) записать систему в матричном виде;

2) найти решение системы с помощью формул Крамера;

3) решить систему при помощи обратной матрицы.

Задача 6. Даны координаты трех векторов 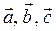 и вектор .

 

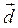№ варианта	Векторы	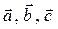Вектор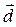
1
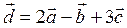
2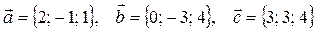
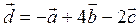
3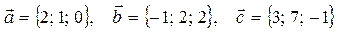
4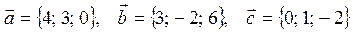
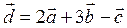
5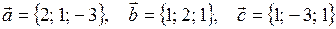
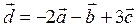
6
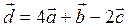
7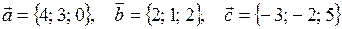
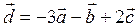
8
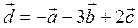
9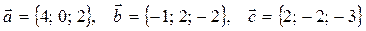
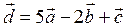
10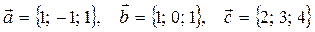

 

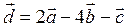
Требуется:

1) вычислить модуль вектора ;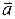

2) найти координаты вектора ;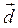

3) найти угол φ между векторам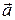и  и ;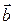

4) вычислить проекцию вектора 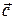 на направление вектора ;

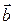5) вычислить площадь треугольника, построенного на векторах  и ;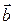

6) вычислить объем параллелепипеда, построенного на векторах .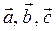

 

Задача 7. Даны координаты точек – вершин пирамиды ABCD.

№ варианта	Координаты точек
1	А (1; 2; –1), В (0; 0; 1),   С (1; –3; 3),   D (2; –1; –1)
2	А (7; 2; 4), В (7; –1; –2),   С (3; 3; 1),   D (4; 2; 1)
3	А (1; 3; 6), В (2; 2; 1),   С (–1; 0; 1),   D (–4; 6; –3)
4	А (–2; 0; –4), В (–1; 7; 1),   С (4; –8; –4),   D (1; –4; 6)
5	А (1; 2; 0), В (3; 0; –1),   С (5; –2; 3),   D (3; 2; –1)
6	А (–1; 1; 2), В (2; 1; –2),   С (–2; 0; 4),   D (2; –1; 2)
7	А (4; 2; 5), В (2; –3; 0),   С (–10; 5; 8),   D (–5; 2; 4)
8	А (2; –1; 1), В (–1; –3; 2), С (–2; 3; 1), D (–1; 2; –3)
9	А (–1; 1; 2), В (–2; 0; 3), С (3; 6; –3), D (–1; –2; 7)
10	А (4; –1; 3), В (–2; 1; 0), С (0; –5; 1), D (–2; 1; –1)

Требуется:

1) вычислить длину ребра AB;

2) найти уравнение плоскости грани ABC;

3) найти угол 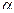 между гранями ABC и BCD;

4) составить параметрические уравнения прямой AB;

5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D;

6) найти координаты точки пересечения DK и грани ABC;

7) найти угол 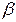 между ребрами AB и BC;

8) найти угол 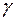 между ребром AD и гранью ABC;

9) сделать чертеж пирамиды в системе координат.