Контрольной работы
Задача 1. Даны координаты вершин треугольника АВС:
А (–3; –1), В (4; 6), С (8; –2).
Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В;
4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.
Задача 2. Дано уравнение кривой 2-го порядка: 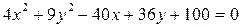 .
.
Привести заданное уравнение к каноническому виду путем параллельного переноса осей координат. Определить тип кривой, найти ее характерные элементы в исходной системе координат. Изобразить на чертеже расположение кривой относительно обеих систем координат.
Задача 3. Даны уравнение кривой 2-го порядка 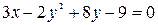 и уравнение прямой l: x + 2 y –3 = 0.
и уравнение прямой l: x + 2 y –3 = 0.
Требуется: 1) привести заданное уравнение кривой 2-го порядка к каноническому виду; 2) найти точки пересечения кривой и заданной прямой; 3) построить обе линии в исходной системе координат.
Задача 4. Даны многочлен f (x) и матрица А:
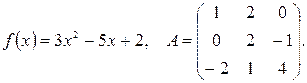
Требуется найти значение матричного многочлена f (A).
Задача 5. Дана система трех линейных алгебраических уравнений с тремя неизвестными: 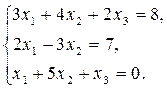
Требуется:
1) записать систему в матричном виде;
2) найти решение системы с помощью формул Крамера;
3) решить систему при помощи обратной матрицы.
Задача 6. Даны координаты трех векторов: 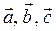 и вектор
и вектор 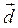 :
:
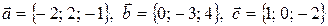 ,
, 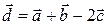 .
.
Требуется:
1) вычислить модуль вектора 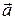 ;
;
2) найти координаты вектора 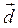 ;
;
3) найти угол φ между векторами 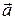 и
и 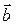 ;
;
4) вычислить проекцию вектора 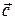 на направление вектора
на направление вектора 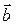 ;
;
5) вычислить площадь треугольника, построенного на векторах 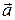 и
и 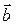 ;
;
6) вычислить объем параллелепипеда, построенного на векторах 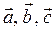 .
.
Задача 7. Даны координаты точек – вершин пирамиды ABCD:
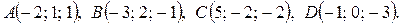
Требуется:
1) вычислить длину ребра AB;
2) найти уравнение плоскости грани ABC;
3) найти угол 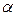 между гранями ABC и BCD;
между гранями ABC и BCD;
4) составить параметрические уравнения прямой AB;
5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D;
6) найти координаты точки пересечения DK и грани ABC;
7) найти угол  между ребрами AB и BC;
между ребрами AB и BC;
8) найти угол 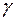 между ребром AD и гранью ABC;
между ребром AD и гранью ABC;
9) сделать чертеж пирамиды в системе координат.
Решение задачи 1.
1) Вычислим длину стороны ВС по формуле (1):
| BС |= 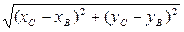 =
= 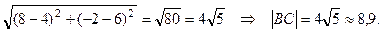
2) Составим уравнение стороны ВС, используя формулу (8):
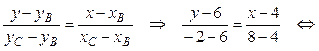
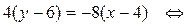
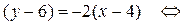 y = –2 x + 14 – уравнение ВС.
y = –2 x + 14 – уравнение ВС.
3) Внутренний угол треугольника при вершине В найдем как угол между прямыми ВА и ВС. Для этого сначала вычислим угловой коэффициент прямой ВА по формуле (7):
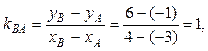
и возьмем из уравнения ВС угловой коэффициент прямой ВС: 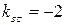 .
.
Из расположения точек A, B, C на координатной плоскости видно, что угол В в треугольнике ABC – острый, поэтому по формуле (11) вычислим

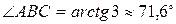 .
.
4) Для получения уравнения высоты АK, проведенной из вершины А, используем уравнение пучка прямых (8) и условие перпендикулярности прямых (10). Сначала вычислим угловой коэффициент прямой АK. Так как 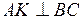 , то
, то 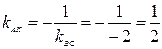 .
.
Уравнение AK получим по формуле (6):
у – уА = kAK (x – x A) 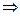 у – (–1) =
у – (–1) = 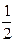 (x – (–3))
(x – (–3)) 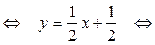
x –2 y + 1 = 0 – уравнение AK.
5) Для определения координат центра тяжести треугольника используем свойство точки пересечения его медиан: если AМ – медиана треугольника и P – точка пересечения его медиан, то P делит AМ в отношении 2: 1, начиная от точки А, т.е. 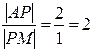 .
.
Основание медианы AМ – точка М является серединой отрезка ВС. Найдем координаты точки М по формулам (3):
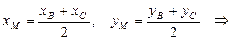
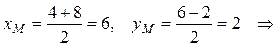 М (6; 2).
М (6; 2).
Теперь, когда координаты концов отрезка AМ известны, найдем координаты точки P, которая делит AМ в отношении 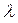 = 2, начиная от точки А, по формулам деления отрезка в заданном отношении (2):
= 2, начиная от точки А, по формулам деления отрезка в заданном отношении (2):
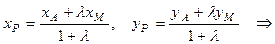

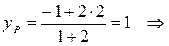
P (3; 1) – центр тяжести треугольника АВС.
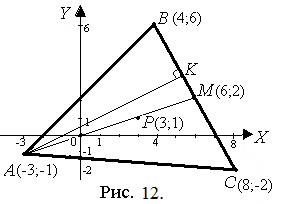
6) Построим чертеж к задаче в системе координат ХОY (рис. 12). Полученные при решении задачи результаты не противоречат чертежу.
Ответы:
1) длина стороны | BС | = 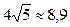 ;
;
2) уравнение стороны ВС: y = –2 x + 14;
3) угол при вершине В: 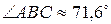 ;
;
4) уравнение высоты АK: x –2 y + 1 = 0;
5) координаты центра тяжести треугольника P (3; 1);
6) чертеж на рис. 12.
Решение задачи 2.
Приведем заданное уравнение кривой 2-го порядка к каноническому виду. Для этого выделим в уравнении полные квадраты по переменным х и у:
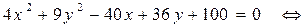
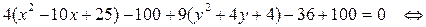
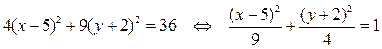 .
.
Получили уравнение эллипса с центром в точке O 1(5; – 2) (см. таблицу 2 в разделе «справочный материал»).
Осуществив параллельный перенос осей координат в системе XOY по формулам: 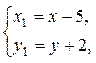 получим каноническое уравнение эллипса
получим каноническое уравнение эллипса 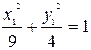 в системе координат X 1 O 1 Y 1 , где O 1(5; –2) в системе XOY (рис. 14).
в системе координат X 1 O 1 Y 1 , где O 1(5; –2) в системе XOY (рис. 14).
Найдем характерные элементы эллипса: 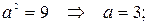
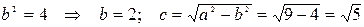 .
.
Отсюда получаем: а = 3 – большая полуось эллипса, b = 2 – малая полуось эллипса, с = 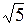 – фокусное расстояние. Координаты фокусов эллипса в системе координат X 1 O 1 Y 1: F 1(–
– фокусное расстояние. Координаты фокусов эллипса в системе координат X 1 O 1 Y 1: F 1(– 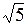 ; 0), F 2(
; 0), F 2(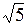 ; 0).
; 0).
Найдем координаты фокусов в системе координат XOY:
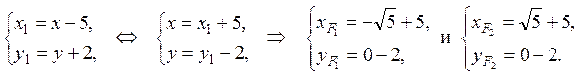
Таким образом, координаты фокусов эллипса в системе координат XOY:
F 1(– 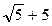 ; –2), F 2(
; –2), F 2(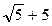 ;–2).
;–2).
 Вычислим эксцентриситет эллипса:
Вычислим эксцентриситет эллипса: 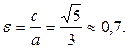
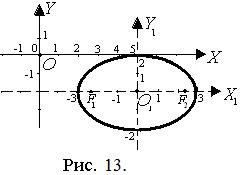
Изобразим на чертеже расположение эллипса относительно обеих систем координат (рис. 13).
Ответ: 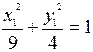 – каноническое уравнение эллипса, где
– каноническое уравнение эллипса, где 
Характерные элементы:
O 1(5; –2) – центр эллипса;
а = 3 – большая полуось эллипса, b = 2 – малая полуось эллипса;
с = 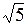 – фокусное расстояние;
– фокусное расстояние;
координаты фокусов эллипса в системе координат XOY: F 1(–  ; –2), F 2(
; –2), F 2(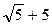 ;–2);
;–2);
эксцентриситет эллипса 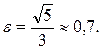
Чертеж на рис. 13.
Решение задачи 3.
1) Приведем заданное уравнение кривой 2-го порядка к каноническому виду. Для этого выделим полный квадрат по переменной у (квадрат переменной х в уравнении отсутствует):
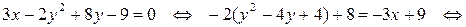
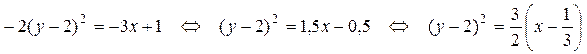 .
.
Получили уравнение параболы вида 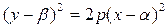 с вершиной в точке
с вершиной в точке 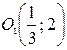 (см. таблицу 2 в разделе «справочный материал»). Осуществим параллельный перенос осей координат по формулам:
(см. таблицу 2 в разделе «справочный материал»). Осуществим параллельный перенос осей координат по формулам: 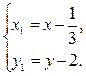 В результате получим каноническое уравнение параболы
В результате получим каноническое уравнение параболы 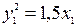 в системе координат X 1 O 1 Y 1.
в системе координат X 1 O 1 Y 1.
2) Найдем точки пересечения параболы и заданной прямой в системе координат XOY. Для этого решим систему уравнений:
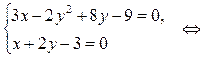
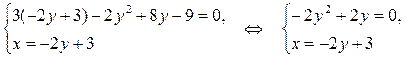
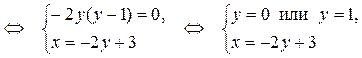
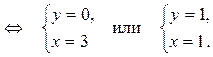
 Таким образом, парабола и прямая пересекаются в точках А (3; 0) и В (1; 1).
Таким образом, парабола и прямая пересекаются в точках А (3; 0) и В (1; 1).
3) Построим обе линии в системе координат XOY (рис. 14).
Ответы: 1) 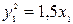 ;
;
2) А (3; 0), В (1; 1);
3) чертеж на рис. 14.
Решение задачи 4.
Записываем матричный многочлен: 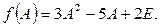 Здесь Е – единичная матрица той же размерности, что и А, т.е. 3-го порядка.
Здесь Е – единичная матрица той же размерности, что и А, т.е. 3-го порядка.
Найдем матрицу A 2. При умножении матрицы A на себя используем правило «строка на столбец» (формула (21)):
A 2 = A·A = 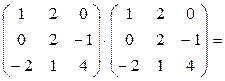
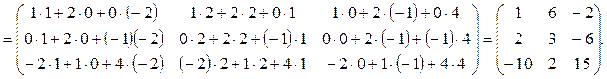
Найдем матрицу 2 Е, используя правило умножения матрицы на число (формула (19)):
E = 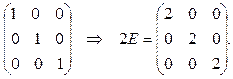
Теперь найдем значение матричного многочлена f (A), используя правило умножения матрицы на число и правило сложения матриц (формула (20)):
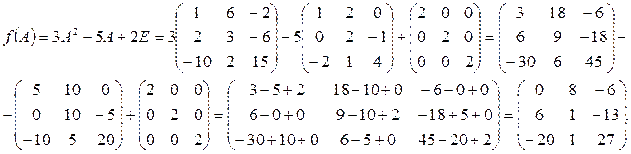
Ответ: 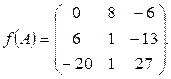
Решение задачи 5.
1) Запишем систему в матричном виде:
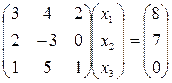 , или AX = B, где
, или AX = B, где 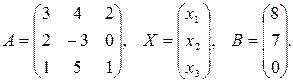
(Во втором уравнении системы отсутствует неизвестная х 3, т.е. а 23 = 0).
2) Решим систему с помощью формул Крамера. Для этого по формулам (27) составляем главный определитель системы из коэффициентов при неизвестных в левых частях уравнений и три вспомогательных определителя:
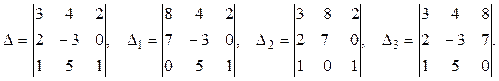
Вычислим эти определители, используя формулу (23):
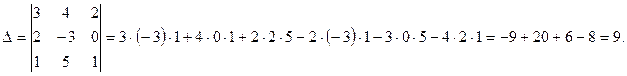
Так как ∆ ≠ 0, то данная система имеет единственное решение.
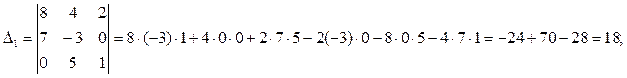
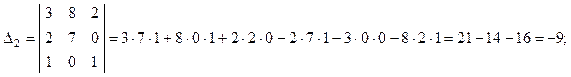
 Найдем решение системы по формулам Крамера (28):
Найдем решение системы по формулам Крамера (28):
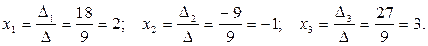
3) Решим систему при помощи обратной матрицы.
a) Определитель 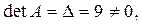 следовательно, обратная матрица существует.
следовательно, обратная матрица существует.
б) Чтобы найти союзную матрицу А * к матрице А, необходимо вычислить по формулам (24) алгебраические дополнения всех ее элементов:
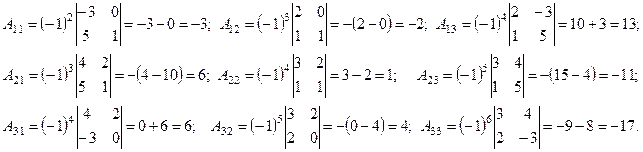 Здесь определители 2-го порядка вычислены по формуле (22).
Здесь определители 2-го порядка вычислены по формуле (22).
Тогда союзная матрица (см. формулу (29)): 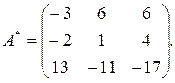
в) Найдем обратную матрицу по формуле (30):
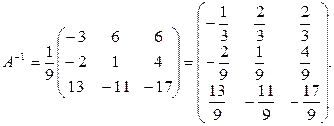
г) Получим решение системы при помощи обратной матрицы по формуле (31) (правило «строка на столбец»):
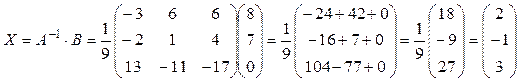
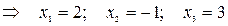 .
.
Решение, полученное матричным способом, совпадает с тем, которое получено по формулам Крамера, что подтверждает правильность этого решения.
Ответы:
1) система в матричном виде: AX = B, где  ;
;
2) решение системы, полученное с помощью формул Крамера:
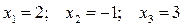 ;
;
3) решение системы, полученное при помощи обратной матрицы:
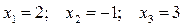 .
.
Решение задачи 6.
1) Модуль вектора  вычисляется по формуле (33):
вычисляется по формуле (33):

 .
.
2) Чтобы найти координаты вектора 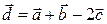 , используем формулы (36) и (37):
, используем формулы (36) и (37):
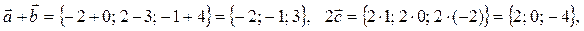
тогда 
3) Косинус угла между векторами 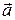 и
и 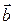 найдем по формуле (39):
найдем по формуле (39):
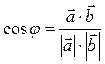 .
.
Для этого вычислим скалярное произведение 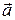 и
и 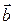 по формуле (38):
по формуле (38): 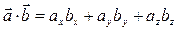 = –2∙0 + 2∙(–3) + (–1)∙4 = –10, затем модуль вектора
= –2∙0 + 2∙(–3) + (–1)∙4 = –10, затем модуль вектора 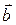 :
: 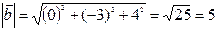 , тогда
, тогда 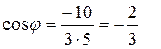 и
и 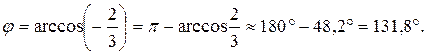
4) Проекцию вектора 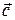 на направление
на направление 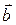 вычислим по формуле (40):
вычислим по формуле (40):
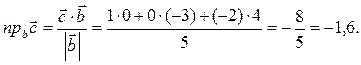
5) Площадь треугольника, построенного на векторах 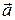 и
и 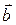 найдем по
найдем по
формуле (42). Для этого сначала находим векторное произведение этих векторов по формуле (41):
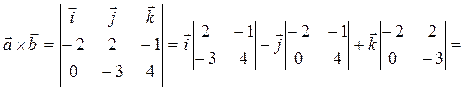
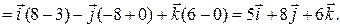
Следовательно, площадь треугольника, построенного на векторах 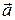 и
и 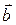 :
:
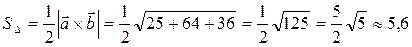 (кв.ед.).
(кв.ед.).
6) Для вычисления объема параллелепипеда, построенного на векторах
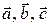 находим смешанное произведение векторов по формуле (43):
находим смешанное произведение векторов по формуле (43):
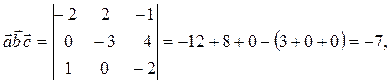
тогда объема параллелепипеда по формуле (47): 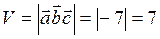 .
.
Ответы:
1) модуль вектора 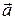 :
: 
2) координаты вектора 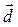 :
: 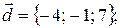
3) угол между векторами 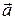 и
и 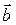 :
: 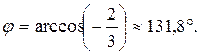
4) проекция вектора 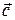 на направление вектора
на направление вектора 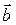 :
: 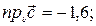
5) площадь треугольника, построенного на векторах 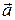 и
и 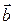 :
: 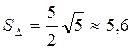 (кв.ед.);
(кв.ед.);
6) объем параллелепипеда, построенного на векторах 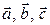 :
: 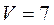 (куб.ед.).
(куб.ед.).
Решение задачи 7.
1) Длину ребра 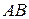 найдем по формуле (34):
найдем по формуле (34):
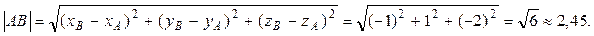
2) Чтобы получить уравнение плоскости грани ABC, необходимо найти вектор, перпендикулярный плоскости ABC, т.е. вектор, перпендикулярный векторам 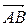 и
и 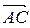 . Одним из таких векторов является векторное произведение
. Одним из таких векторов является векторное произведение 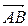 на
на 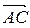 . Для того, чтобы найти его, сначала вычислим координаты векторов по формуле (35):
. Для того, чтобы найти его, сначала вычислим координаты векторов по формуле (35):
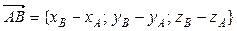 ={–3–(–2); 2–1; –1–1} = {–1; 1; –2},
={–3–(–2); 2–1; –1–1} = {–1; 1; –2},
 ={7; –3; –3}.
={7; –3; –3}.
Векторное произведение 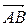 и
и 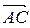 найдем по формуле (41):
найдем по формуле (41):
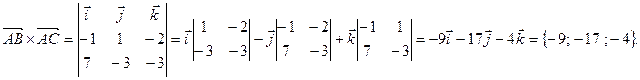 В качестве вектора нормали к плоскости ABC можно взять любой вектор, коллинеарный полученному, например,
В качестве вектора нормали к плоскости ABC можно взять любой вектор, коллинеарный полученному, например, 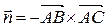 = {9; 17; 4}. Используем уравнение плоскости, проходящей через точку
= {9; 17; 4}. Используем уравнение плоскости, проходящей через точку 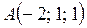 перпендикулярно вектору
перпендикулярно вектору 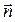 (формула (46):
(формула (46): 
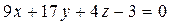 – уравнение плоскости грани ABC.
– уравнение плоскости грани ABC.
3) Прежде, чем найти угол 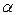 между гранями ABC и BCD, получим уравнение грани BCD, используя уравнение плоскости, проходящей через три заданные точки
между гранями ABC и BCD, получим уравнение грани BCD, используя уравнение плоскости, проходящей через три заданные точки 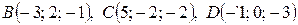 (формула (47):
(формула (47):
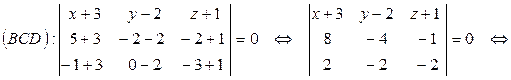
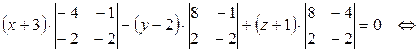
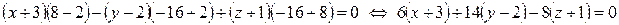
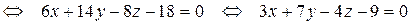 – уравнение грани BCD.
– уравнение грани BCD.
Из уравнения плоскости BCD возьмем координаты вектора нормали  , перпендикулярного этой плоскости:
, перпендикулярного этой плоскости: 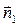 ={3; 7; –4}.
={3; 7; –4}.
Косинус угла 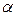 между плоскостями (гранями) ABC и BCD найдем по формуле(48):
между плоскостями (гранями) ABC и BCD найдем по формуле(48):

Отсюда 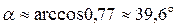 .
.
4) Уравнения ребра AB можно записать как параметрические уравнения прямой, проходящей через точку A (–2;1;1) и имеющей направляющий вектор 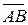 = {–1; 1; –2} (формулы (49)):
= {–1; 1; –2} (формулы (49)):
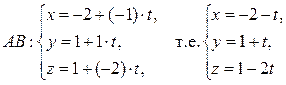 – параметрические уравнения AB.
– параметрические уравнения AB.
Другой способ: можно использовать уравнения прямой, проходящей через две точки 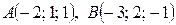 (формулы (51)):
(формулы (51)):
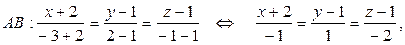
откуда, обозначив каждую из дробей буквой t, получаем:
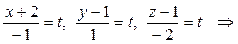
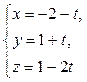 – параметрические уравнения AB.
– параметрические уравнения AB.
5) Высота пирамиды DK – это прямая, проведенная из вершины D перпендикулярно грани ABC. Она имеет направляющий вектор 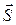 , коллинеарный вектору нормали плоскости ABC. Можно взять, например,
, коллинеарный вектору нормали плоскости ABC. Можно взять, например,  =
= 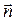 = {9; 17; 4}. Запишем канонические уравнения высоты DK, используя точку D (–1; 0; –3) и вектор
= {9; 17; 4}. Запишем канонические уравнения высоты DK, используя точку D (–1; 0; –3) и вектор 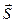 ={9; 17; 4} (формулы (50)):
={9; 17; 4} (формулы (50)):
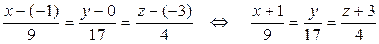 – канонические уравнения DK.
– канонические уравнения DK.
6) Прежде, чем найти точку пересечения DK и грани ABC, получим параметрические уравнения прямой DK. Обозначив каждую из дробей в канонических уравнениях буквой t, получаем:
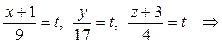
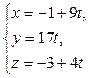 – параметрические уравнения DK.
– параметрические уравнения DK.
Точка пересечения DK и грани ABC (точка К) лежит на прямой, а значит, имеет координаты 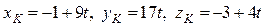 , и принадлежит плоскости, т.е. ее координаты удовлетворяют уравнению плоскости ABC. Поэтому координаты точки K найдем, решив систему:
, и принадлежит плоскости, т.е. ее координаты удовлетворяют уравнению плоскости ABC. Поэтому координаты точки K найдем, решив систему:
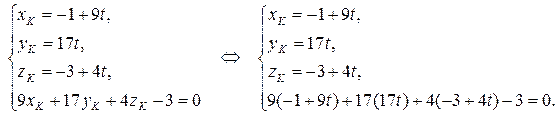
Решим последнее уравнение относительно t:
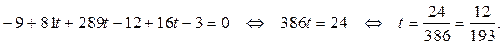
Вычислим координаты точки K, подставив найденное значение параметра t в первые три уравнения системы:
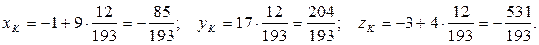

Итак, точка пересечения DK и грани ABC:  .
.
7) Угол 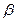 между ребрами AB и BC найдем, как угол между направляющими векторами прямых AB и BC:
между ребрами AB и BC найдем, как угол между направляющими векторами прямых AB и BC: 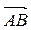 = {–1; 1; –2} и
= {–1; 1; –2} и 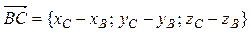 ={8; –4; –1}. Вычислим косинус угла
={8; –4; –1}. Вычислим косинус угла 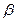 по формуле (52):
по формуле (52):
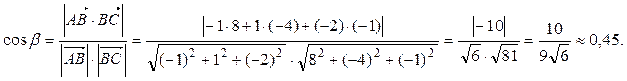
Тогда угол между ребрами AB и BC: 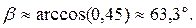
8) Чтобы определить угол 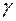 между ребром AD и гранью ABC, найдем направляющий вектор прямой:
между ребром AD и гранью ABC, найдем направляющий вектор прямой: 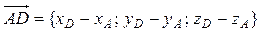 ={1; –1; –4}. Плоскость ABC имеет вектор нормали
={1; –1; –4}. Плоскость ABC имеет вектор нормали 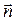 = {9; 17; 4}. Синус угла
= {9; 17; 4}. Синус угла  между прямой
между прямой  и плоскостью ABC можно вычислить по формуле (53):
и плоскостью ABC можно вычислить по формуле (53):
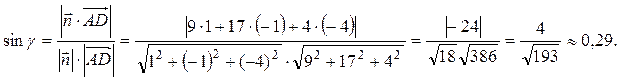
Тогда угол между ребром AD и гранью ABC: 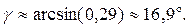
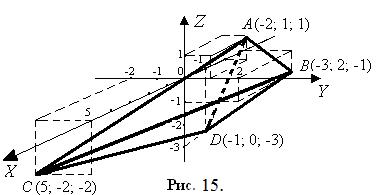
9) Выполним чертеж пирамиды в системе координат (рис. 15).
Ответы:
1) 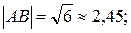
2) АВС: 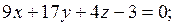
3) 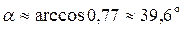 ;
;
4) 
5) DK:  ; 6)
; 6) 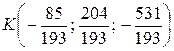 ;
;
7) 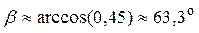 ; 8)
; 8)  ;
;
9) чертеж пирамиды на рис. 15.
 2020-06-30
2020-06-30 87
87








