· Рассмотреть свойства арксинуса и арккосинуса;
· Рассмотреть свойства арктангенса и арккотангенса;
· Объяснять расположение промежутков монотонности;
· Определять наибольшее и наименьшее значение функции;
· Применять знания при решении задач.
Глоссарий по теме
Арксинус (y = arcsin x) – это функция, обратная к синусу (x = sin y). Он имеет область определения 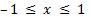 и множество значений
и множество значений 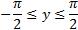 .
.
Арккосинус (y = arccos x) – это функция, обратная к косинусу (x = cos y). Он имеет область определения 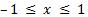 и множество значений
и множество значений 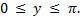
Арктангенс (y = arctg x) – это функция, обратная к тангенсу (x = tg y). Он имеет область определения 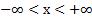 и множество значений
и множество значений 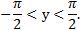 .
.
Арккотангенс (y = arcctg x) – это функция, обратная к котангенсу (x = ctg y). Он имеет область определения 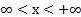 и множество значений
и множество значений 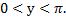
Обратные тригонометрические функции решают задачу вычисления углов по известному значению тригонометрической функции. Например, косинус какого угла равен  ? Первое, что хочется ответить, что это угол 60° или
? Первое, что хочется ответить, что это угол 60° или  , но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен
, но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен  , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.
, бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.
Рассмотрим свойства функции y=arcsin x и построим ее график.
Арксинус (y = arcsin x) – это функция, обратная к синусу (x = sin y).
| Свойства | Функции y=arcsin х |
| E(f) | 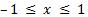
|
| D(f) | 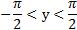
|
| Чётность | Нечётная, т.к. arcsin(-x)= - arcsin x |
| Промежутки монотонности | Возрастающая |
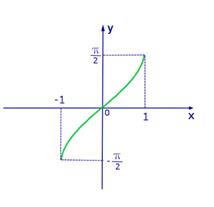 Рис.1 График функции y=arcsin х
Рис.1 График функции y=arcsin х
Рассмотрим свойства функции y=arcos x и построим ее график.
Арккосинус (y = arccos x) – это функция, обратная к косинусу (x = cos y).
| Свойства | Функции y=arccos х |
| E(f) | 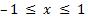
|
| D(f) | 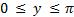
|
| Чётность | Ни чётная, ни нечётная |
| Промежутки монотонности | Убывающая |
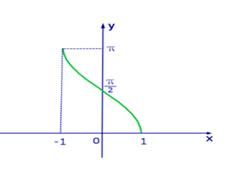 Рис.2 График функции y=arccos х
Рис.2 График функции y=arccos х
Рассмотрим свойства функции y=arctgx и y=arcctgx и построим их графики.
Арктангенс (y = arctg x) – это функция, обратная к тангенсу (x = tg y).
Арккотангенс (y = arcctg x) – это функция, обратная к котангенсу (x= ctg y).
| Свойства | y=arctg х | y=arcctg х |
| E(f) | R | R |
| D(f) | 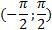
| 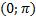
|
| Чётность | Нечётная | Нечётная |
| Промежутки монотонности | Возрастающая | Убывающая |
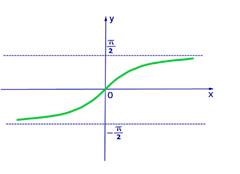 Рис.3 График функции y=arctgx
Рис.3 График функции y=arctgx
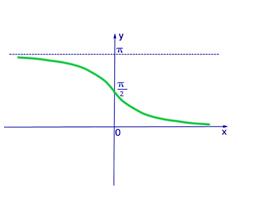 Рис.4 График функции y=arcсtgx
Рис.4 График функции y=arcсtgx
Пример 1. Найдите значение выражения 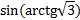
Обозначим 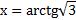 , по определения арктангенса получаем х=60°, т.е. нам нужно найти
, по определения арктангенса получаем х=60°, т.е. нам нужно найти 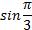
Ответ: 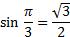
Пример 2. Решите неравенство 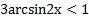
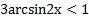 ;
;
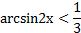 ;
;
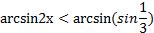 ;
;
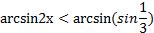 ;
;
Накладываем ограничения по свойствам арксинуса:
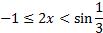 ;
;
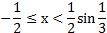
Ответ: 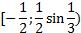
 2020-07-01
2020-07-01 154
154







