Расчёт спектра сигнала

2.1. Нарисовать в масштабе временную реализацию сигнала. Рассчитать и построить спектр сигнала, для этого определить коэффициенты 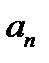, , 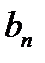, , 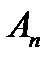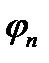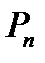. Определить эффективную ширину спектра. Восстановить сигнал по сумме гармоник.

U=4 В

N_Ф1=4

N_Ф2=6

N_Ф3=4

Q=6

T=0,006 с

𝜏_И=2,3

N_Ф1+ N_Ф2=10 выбираем четную последовательность прямоугольных импульсов.

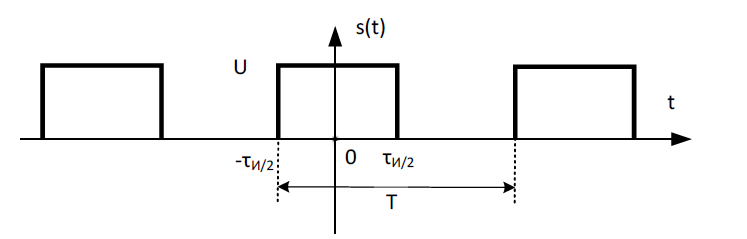
Рисунок 7 – График S(t)

Таблица 3 – Сводная таблица

n	1	2	3	4	5	6	7	8	9
Частота n/T, Гц	166	332	498	664	830	996	1162	1328	1500
A0=a0/2, В	0,6
an, В	0,6	1,1	0,55	5,19*10-6	-0,27	-0,22	-5,19*10-6	0,15	0,13
bn, В	0
An, В	0,6	1,1	0,55	5,19*10-6	-0,27	-0,22	-5,19*10-6	0,15	0,13
φn, рад	0
P, В2	3
P0, В2	0,4
Pn, В2	0,4	0,6	0,15	1,35*10-6	0,03	0,02	1,35*10-6	0,012	0,01

Построим требуемые графики.

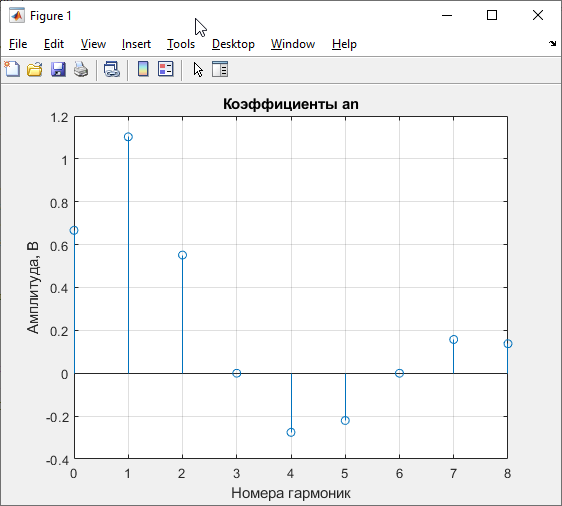
Рисунок 8 – График коэффициентов an

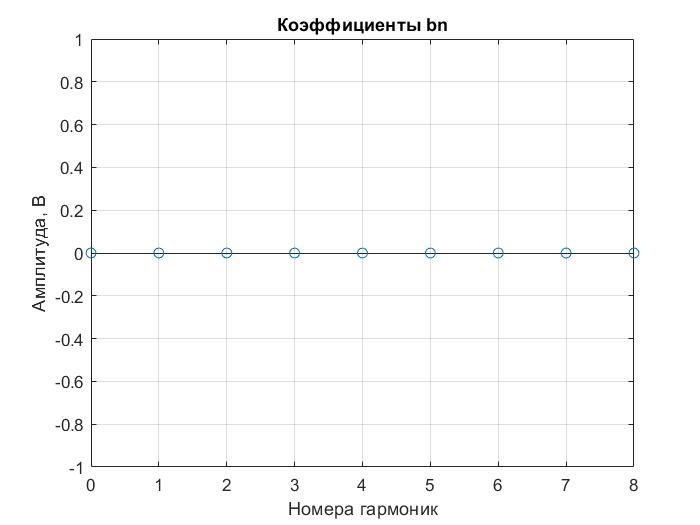
Рисунок 9 – График коэффициентов bn

 

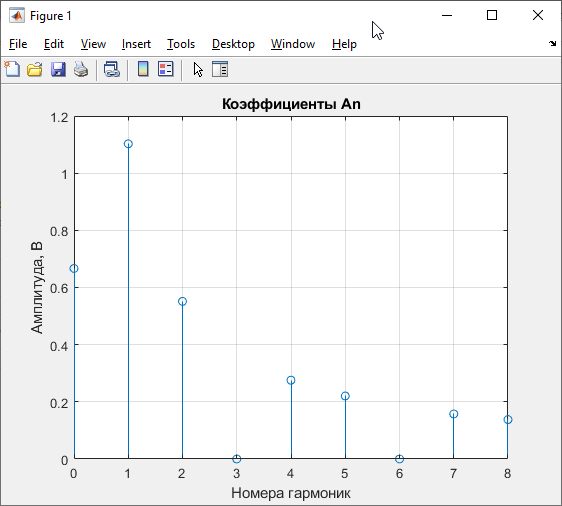
Рисунок 10 – График коэффициентов An

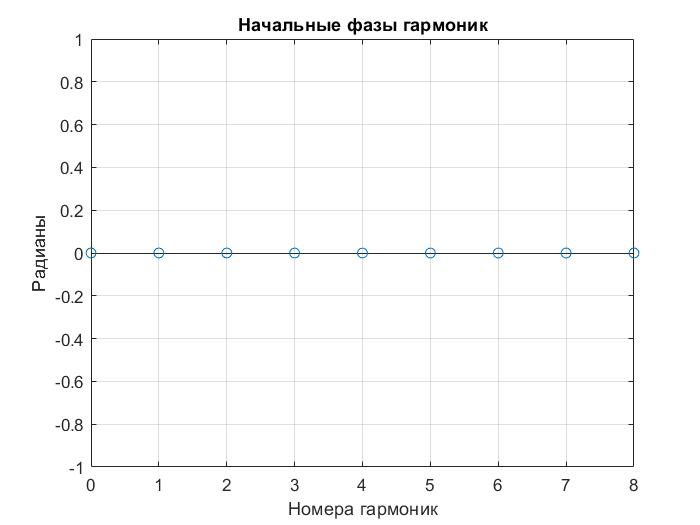
Рисунок 11 – График начальных фаз гармоник

 

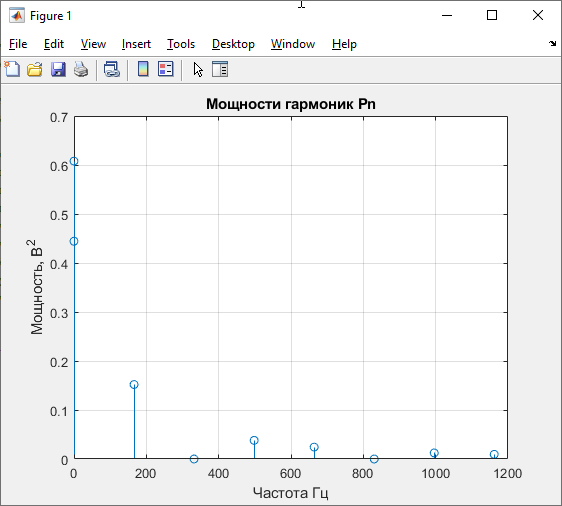
Рисунок 12 – График мощностей гармоник Рn

2.2. Моделирование процесса восстановления сигнала.

P_s=2,2 В² При N=8;

Ps=0,9P=2,3 В²; Ширина спектра=332, f=332 Гц;

Проведем моделирование в MatLAB.

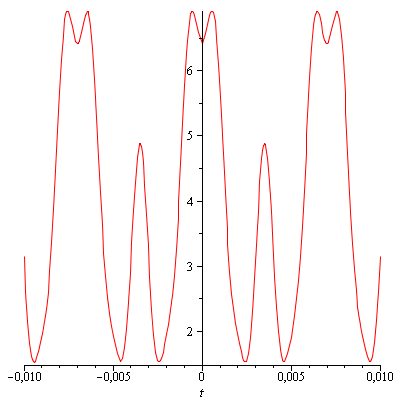
Рисунок 13 – График процесса восстановления сигнала

При N→∞ форма сигнала после сумматора будет соответствовать исходной последовательности прямоугольных импульсов.

Расчёт информационных параметров сообщения

3.1. Определить энтропию, количество информации и избыточность сообщения из Фамилии Имени Отчества студента.

Войнов Алексей Александрович

N=22

В о й н а л е к а л е к с

M=14

Р(в)=3/22, р(о)=2/22, р(й)=2/22, р(н)=1/22, р(о)=2/22, р(а)=1/22, р(л)=1/22, р(е)=4/22, р(р)=1/22, р(г)=1/22, р(и)=1/22, р(ч)=1/22, р(с)=2/22

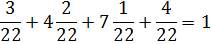
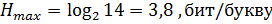
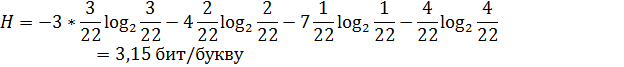
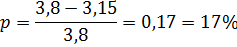
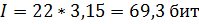
ЗАДАНИЕ 3.2

Буква фамилии	Двоичный код
В	0100 0011 0010
о	0100 0011 1110
й	0100 0011 1000
н	0100 0011 1101
о	0100 0011 1110
в	0100 0011 0010

Таблица 4 – Сводная таблица данных

 

0100 0011 0010 0100 0011 1110 0100 0011 1000 0100 0011 1101 0100 0011 1110 0100 0011 0010

n(0)=40 n(1)=31

p(0)+p(1)=1

n(01)=17

n(00)=30

n(11)=19

n(10)=18

p(0/0)=30/46=0,65

p(1/0)=17/46=0,35

p(0/1)=18/37=0,49

p(1/1)=19/37=0,51

 

p(0/0)+p(1/0)=1

p(0/1)+p(1/1)=1

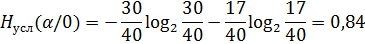
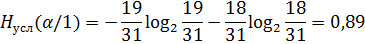
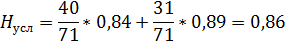
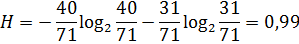
Условие соблюдается:0,86<0,99