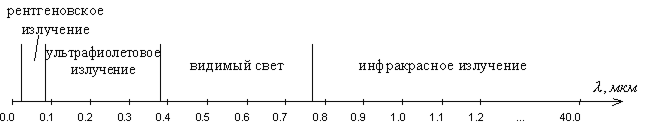
Описание световых волн
Основные свойства световых полей
Световое поле – это электромагнитное поле в оптическом диапазоне частот:
Уравнения Максвелла
Основными величинами, определяющими электромагнитное поле, являются:
- вектор электрической напряженности поля:
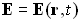 ,
,  ,
,
- вектор магнитной напряженности поля:
 ,
,  ,
,
где  – время,
– время,  – радиус-вектор.
– радиус-вектор.
В среде, отличной от вакуума, под действием электромагнитного поля возникают:
- электрическая индукция:
 ,
,  ,
, - магнитная индукция:
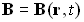 ,
, 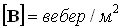 .
.
В уравнения Максвелла кроме указанных величин входят:
- объемная плотность заряда:
 ,
,  ,
, - поверхностная плотность тока:
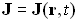 ,
, 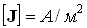 ,
, - электрическая проницаемость среды:
 ,
, - магнитная проницаемость среды:
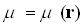 .
.
Уравнения Максвелла (Maxwell's equations):
| в общем виде | в диэлектрической среде | ||||||||||||||||||||||||||||||||||||||
| операторная форма записи | классическая форма записи | ||||||||||||||||||||||||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||
Уравнения (5-6) называют материальными уравнениями, так как они учитывают свойства вещества.
В вакууме и диэлектриках, плотность заряда и токи равны нулю:  .
.
Электрическая  и магнитная
и магнитная 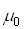 проницаемости в вакууме связаны со скоростью света следующим соотношением:
проницаемости в вакууме связаны со скоростью света следующим соотношением:
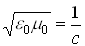
где  – скорость распространения электромагнитного излучения в вакууме.
– скорость распространения электромагнитного излучения в вакууме.
Для оптических частот 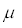 =
= 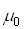 .
.
Отношение скорости света в вакууме к скорости света в среде называется показателем преломления данной среды по отношению к вакууму (index of refraction):
|
где  – скорость света в среде,
– скорость света в среде,  – скорость света в вакууме.
– скорость света в вакууме.
Световое поле является поперечным (вектор электрической напряженности перпендикулярен вектору магнитной напряженности, и оба они перпендикулярны направлению распространения света).
Математическое описание электромагнитных волн
Для случая линейных и однородных сред вместо уравнений Максвелла можно использовать волновые уравнения.
Волновые уравнения
В скалярной теории электрическое и магнитное поля могут быть описаны независимо друг от друга, а волновые уравнения одинаковы для векторного и скалярного полей.
| волновое уравнение для электрической составляющей поля | волновое уравнение для магнитной составляющей поля | ||||||
|
|
Волновое уравнение в общем виде:
| (1.3.5) |
где  – любая из составляющих электрического вектора или возмущение поля в какой-то точке пространства в какой-то момент времени,
– любая из составляющих электрического вектора или возмущение поля в какой-то точке пространства в какой-то момент времени,
 – вторая производная возмущения по пространственным координатам,
– вторая производная возмущения по пространственным координатам,
 – вторая производная возмущения по времени.
– вторая производная возмущения по времени.
Монохроматическое поле
| Монохроматическое поле – это поле, зависящее от времени по гармоническому закону: |
| ||
| |||
| где | |||
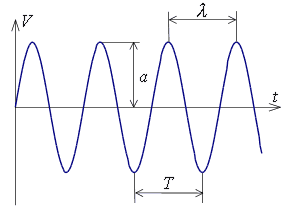
Характеристики монохроматического поля:
- период колебаний
 ,
, 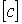 ;
; - частота
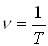 ,
, 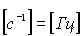 ;
; - циклическая частота
 ,
,  ;
; - длина волны
 :
: 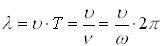 ,
,  или
или  или
или 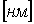 ;
; - волновое число:
 .
.
Волновое возмущение можно записать через эйконал поля 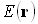 :
:
|
Эйконал поля – фаза светового поля, выраженная как оптическая длина хода лучей данного пучка.
|
Оптическая длина луча 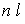 (optical path difference, OPD) – это произведение показателя преломления
(optical path difference, OPD) – это произведение показателя преломления  на геометрическую длину пути
на геометрическую длину пути  . Приращение эйконала равно оптической длине луча:
. Приращение эйконала равно оптической длине луча:
|
 2020-07-01
2020-07-01 351
351
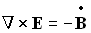
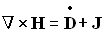

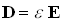


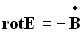
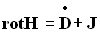






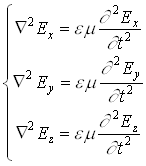
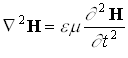
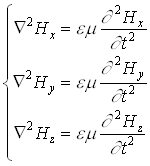


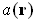 – амплитуда возмущения (функция пространственных координат),
– амплитуда возмущения (функция пространственных координат), 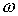 – циклическая частота изменения поля во времени,
– циклическая частота изменения поля во времени, 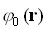 – фаза поля (функция пространственных координат).
– фаза поля (функция пространственных координат).
 ,
, 








