2020-07-01
684
«КИНЕМАТИКА, ДИНАМИКА И ЗАКОНЫ СОХРАНЕНИЯ»
Грузы массами m 1 и m 2 движутся поступательно. К грузам прикреплены невесомые нерастяжимые нити, перекинутые или намотанные на блоки массами m 3 и m 4, которые могут без трения вращаться вокруг горизонтальных осей. Блок массой m 3 – сплошной цилиндр, а блок массой m 4 – ступенчатый цилиндр с радиусами ступеней r 4 и R 4 и одинаковой высотой. При движении по блокам нити не проскальзывают, участки нитей для тел на наклонных плоскостях параллельны этим плоскостям, коэффициент трения тел о любую плоскость равен μ. Система начинает движение из состояния покоя. Считая, что все нити и участки плоскостей имеют достаточную длину, выполнить следующие задания:
1. Найти ускорения грузов массами m 1 и m 2 и угловые ускорения блоков ε3, ε4. Принять r 3= r 4.
2. Найти силы натяжения всех нитей.
3. Используя кинематические формулы, найти скорости грузов, угловые скорости блоков и пути, пройденные грузами спустя время τ после начала движения.
4. Используя закон изменения механической энергии, найти скорости грузов и угловые скорости блоков в тот момент, когда пути, пройденные грузами, составят значения, найдены в п. 3.
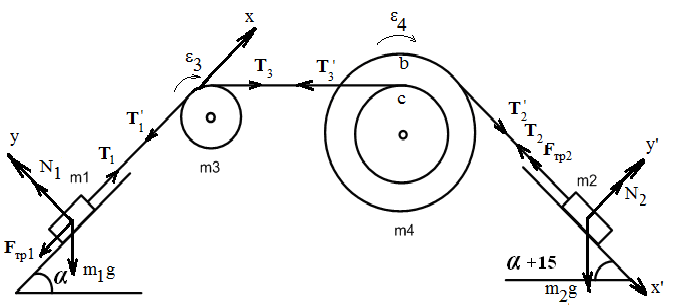
m1 ½
m2 ½
m3 ½
m4 ½
α ½
µ ½
r4 = r3 ½
R4 ½
Τ ½
1. Найти ускорения грузов массами m 1 и m 2 и угловые ускорения блоков ε3, ε4. Принять r 3= r 4.
Запишем 2-й закон Ньютона для тела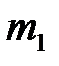 
: 
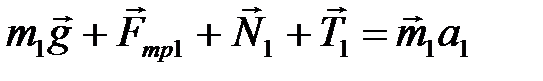(1)
для тела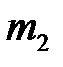 
: 
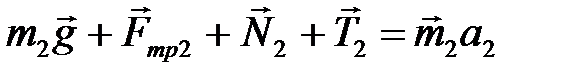(2)
Запишем уравнение динамики вращательного движения для блока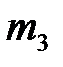 
:
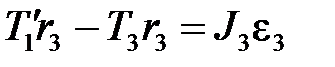; для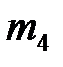 
: 
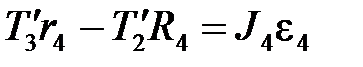
т.к. нить невесома, то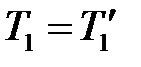 
; 
; 
; 
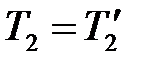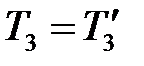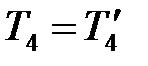
Запишем (1) и (2) в проекции на ох и оу:
груз 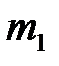: ох: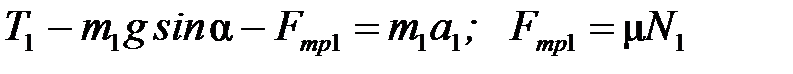 
оу: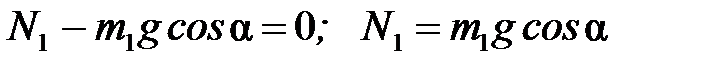 
Тогда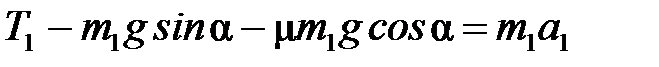 
(3)
груз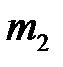 
: 
: 
: 
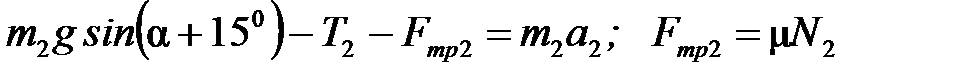
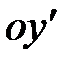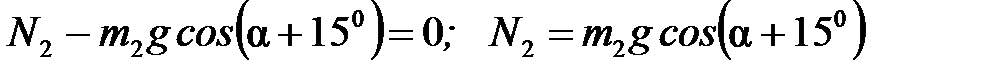
Тогда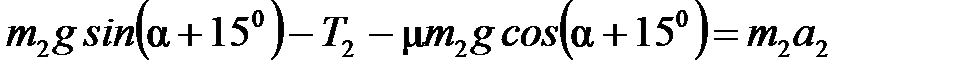 
(4)
Определим момент инерции блока 3: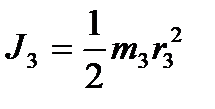 
Определим момент инерции блока 4 – ступенчатого цилиндра
| 
|
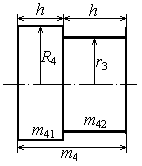
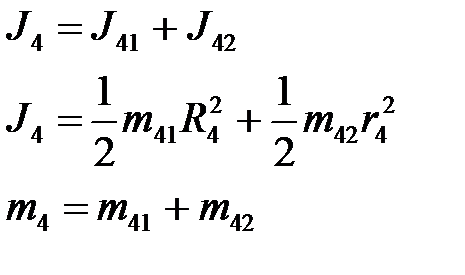
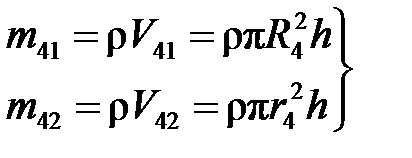
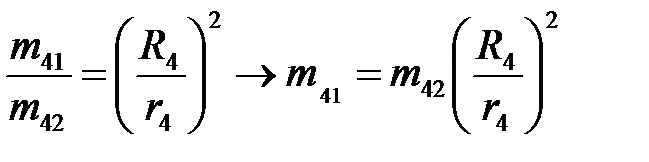
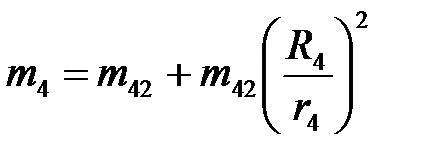; Выразим и рассчитаем m42 и m41
Рассчитаем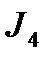 
Выразим а 2 через а 1. Для этого учтем, что угловые ускорения для точек,, в ” и,, c ”: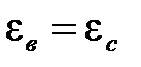 
; 
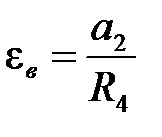
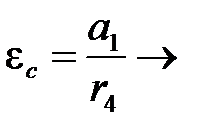
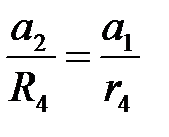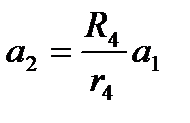
Учтем, что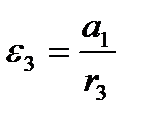 
и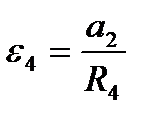 
Уравнения (3) и (4) примут вид:
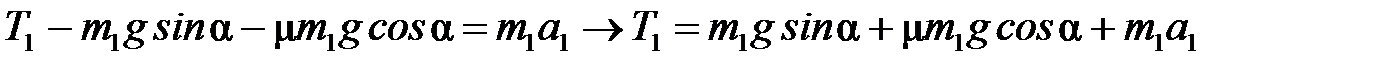
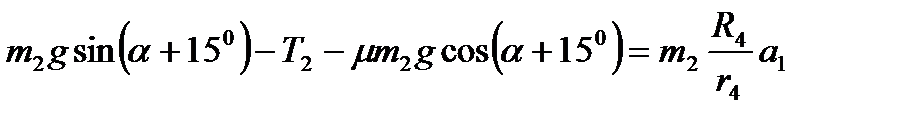
Выразим из уравнения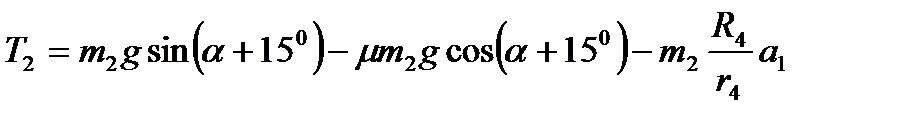 
Уравнения динамики вращательного движения примут вид:
(*)
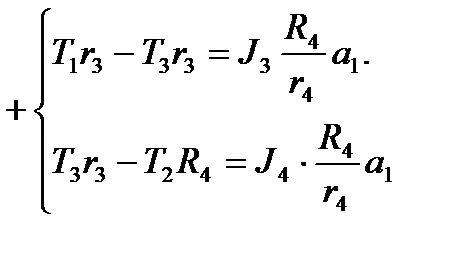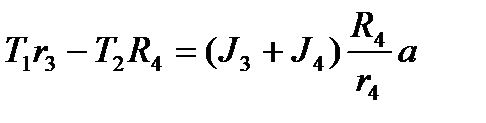(5)
Подставим в (5) выражения для Т1 и Т2:
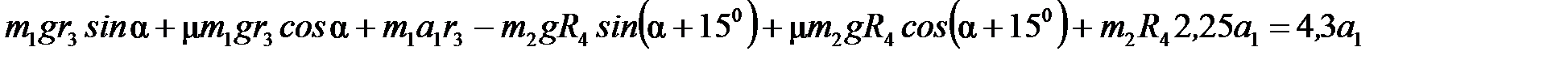Проведя подстановку и расчеты, найдем а1; а2; ɛ3; ɛ4
