Характеристики икосаэдра

Радиус описанной сферы икосаэдра , где a - длина стороны.

Радиус вписанной сферы икосаэдра

Площадь поверхности икосаэдра

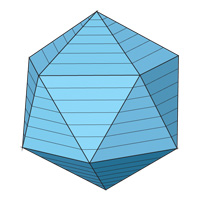  Объем икосаэдра

ДОДЕКАЭДР

 

Древние греки дали многограннику имя по числу граней. «Додека» означает двенадцать, «хедра» - означает грань (додекаэдр двенадцатигранник).

Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел.

Додекаэдр имеет следующие характеристики:

ü Тип грани – правильный пятиугольник

ü Число сторон у грани – 5

ü Общее число граней – 12

ü Число рёбер примыкающих к вершине – 3

ü Общее число вершин – 20

ü Общее число рёбер – 30

Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324°.

Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.

Характеристики додекаэдра

Радиус описанной сферы додекаэдра , где a - длина стороны.

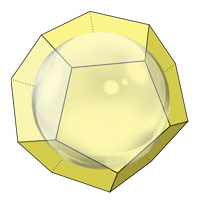Радиус вписанной сферы додекаэдра

    Площадь поверхности додекаэдра

                 Объем додекаэдра 

 

ПРАВИЛЬНЫЙ МНОГОГРАННИК - выпуклый многогранник, грани которого являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине которого сходится одно и то же число ребер.

Правильный многогранник	Число
	граней	вершин	рёбер	(Г + В) - Р
Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр

Вывод: Число граней плюс число вершин минус число рёбер в любом многограннике равно 2.

Формула Эйлера: Сумма числа граней и вершин любого многогранника

равна числу рёбер, увеличенному на 2. (Г + В = Р + 2)

Задание. Определите количество граней, вершин и рёбер многогранника, изображённого на рисунке. Проверьте выполнимость формулы Эйлера для данного многогранника.