Площадь боковой поверхности призмы

Математика

Преподаватель Пронина Е.А.

prokaterina13@yandex.ru

Задание для I курса

 Группы 11-ЭТ, 11 – ОП, 11 – СД

Выполнить в срок до 10 апреля 2020

Выполненную работу отправьте по email prokaterina13@yandex.ru

в виде файла MS WORD.

Для этого создайте новый документ MS Word. Оформите решения в виде формул (вкладка ВСТАВКА –> )

 

Или оформите решения в тетради в вышлите фото на email преподавателя.

Работа должна быть выполнена до 10 апреля.

Не забудьте указать свои Фамилию Имя и группу!

Задания здесь: https://vk.com/id6255441

ВАМ НЕОБХОДИМО:

Составить конспект по темам 1, 2.

Ознакомиться с примерами решения и выполнить задания для самостоятельного решения.

Тема 1.   Многогранники. Призма.

Повторим основные сведения о многогранниках. Особенное внимание уделим определению призмы. Вспомним теорему о площади боковой поверхности прямой призмы.

Повторение, призма

На рисунке 1 изображена призма ABCDFA₁B₁C₁D₁F₁, ее основания ABCDF и A₁B₁C₁D₁F₁. Пятиугольники ABCDF и A₁B₁C₁D₁F₁ равны и лежат в параллельных плоскостях.

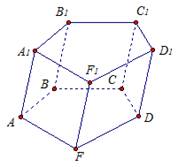
Рис. 1

Призма – это многогранник, в основаниях которого лежат равные многоугольники, а боковые грани – параллелограммы.

Основания призмы – это две грани, являющиеся равными многоугольниками, которые лежат в параллельных плоскостях.

Боковыми гранями являются все грани призмы, кроме оснований. Каждая боковая грань является параллелограммом.

Общие стороны боковых граней называются боковыми ребрами.

Вернемся к рисунку 1. В пятиугольнике ABCDFA₁B₁C₁D₁F₁:

ABCDF и A₁B₁C₁D₁F₁ – основания призмы.

Боковыми гранями являются грани АА₁В₁В, ВВ₁С₁С,CC₁D₁D,DD₁F₁F,FF₁A₁A, а боковыми ребрами – АА₁, ВВ₁, СС₁,DD₁,FF₁.

Прямая призма

Определение. Если боковое ребро призмы перпендикулярно плоскости ее основания, то такая призма называется прямой.

Рассмотрим пятиугольную призму ABCDFA₁B₁C₁D₁F₁ (рис. 2).

Пусть боковое ребро AA₁ перпендикулярно плоскости основания. Значит, данная призма – прямая. Так как ребро АА₁ перпендикулярно плоскости АВС, то это боковое ребро перпендикулярно любой прямой из плоскости основания АВС, в том числе и прямой AF. Значит, боковая грань является прямоугольником.

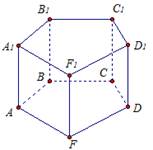Рис. 2

Параллелепипед

Рассмотрим параллелепипед ABCDA₁B₁C₁D_1­ (рис. 3) – частный случай призмы. В основаниях призмы лежат параллелограммы ABCD и A₁B₁C₁D₁.

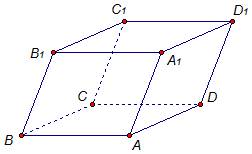
Рис. 3

Если боковое ребро перпендикулярно плоскости основания, то такой параллелепипед будет называться прямым параллелепипедом.

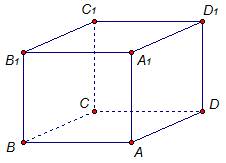
Рис. 4

Рассмотрим параллелепипед ABCDA₁B₁C₁D_1­ (рис. 4). Если ребро AA₁ перпендикулярно плоскости ABCD, то параллелепипед ABCDA₁B₁C₁D_1­ прямой.

Если в основании прямого параллелепипеда лежит прямоугольник, то такой параллелепипед называется прямоугольным. Обозначение: ABCDA₁B₁C₁D_1­ или кратко AC₁.

Правильная призма

Определение. Правильной n -угольной призмой называется такая прямая призма, у которой в основаниях лежит правильный n -угольник.

Площадь боковой поверхности призмы

Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Рассмотрим эту теорему на примере треугольной прямой призмы ABCA₁B₁C₁ (рис. 5). Призма ABCA₁B₁C_1­ – прямая, значит, все боковые ребра перпендикулярны плоскости основания.

Дано: АВСА₁В₁С₁ – прямая призма, т. е. АА₁ ⊥ АВС, АА₁= h.

Доказать: S_бок= Р_осн∙ h.

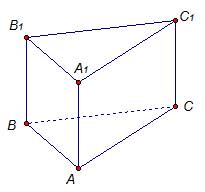
Рис. 5

Доказательство.

Треугольная призма АВСА₁В₁С₁ – прямая, значит, боковые грани АА₁В₁В, АА₁С₁С, ВВ₁С₁С – прямоугольники. А все боковые ребра призмы равны высоте призмы.

Найдем площадь боковой поверхности как сумму площадей прямоугольников АА₁В₁В, АА₁С₁С, ВВ₁С₁С:

S_бок = АВ∙ АА₁+ ВС∙ ВВ₁+ СА∙ СС₁= АВ∙ h + ВС∙ h + СА∙ h = (AB + ВС + CА) ∙ h = P_осн∙ h.

Получаем, S_бок= Р_осн∙ h, что и требовалось доказать.