Модель виброакустического сигнала

Математическим образом сигнала служит функция времени s (t), за­данная на интервале [0, T ]. Способность сигнала предоставлять информацию о состоянии объекта обусловлена тем, что некоторые его свойства имеют возможность изменяться в зависимости от изменения состояния. Для того чтобы диагностическая задача была разрешимой, различным состояниям объекта должны соответствовать различные сигналы, причем это соответст­вие должно быть взаимно однозначным. При этом необходимо установить, чем могут отличаться друг от друга сигналы и как количественно оценить их различие. Этот вопрос сводится к выяснению различия между собой функ­ций.

С понятием функции y = f (x) обычно связывают три элемента:

1) независимую переменную x;

2) зависимую переменную y;

3) правило f, устанавливающее зависимость величины y от значений величины x.

В элементарном анализе существенным считается способность величин x и y изменяться, а правило f считается каждый раз заданным и неизменным при рассмотрении. Объектом исследования являются отдельные функции.

В данном случае придется отойти от такого взгляда на функцию. Функ­цию целесообразно представлять в виде единого объекта, обладающего некоторыми признаками, которые позволяют отличить одну функцию от дру­гой. Таким образом, существенна возможность изменения самого правила f, выражающего функциональную зависимость. Вопрос о характере измене­ния величин x и y отходит на второй план. Это связано с тем, что информа­ция, которую переносят сигналы, заключена в правиле f, устанавливающем зависимость между переменными величинами.

При таком рассмотрении исходным понятием является не индивиду­альная функция, а класс функций, заданный определенным образом. Различ­ные сигналы – это функции, принадлежащие определенному классу. Поэтому вопрос о передачи информации сигналами – это вопрос об изменении функ­ций. Для формирования диагностических признаков дефектов и неисправно­стей необходимо установить, в чем проявляется отличие функций.

Класс диагностических сигналов обычно задают двумя параметрами: длительностью сигнала T и шириной спектра Δf_c = [ f_н, f_в ], где f_н – нижнее значение частоты, f_в – верхнее значение частот диагностируемого объекта. Значение этих параметров устанавливается для данного класса объектов. При выборе T обычно приходится принимать компромиссное решение. Чем больше дли­тельность анализируемого сигнала, тем более полные и надежные сведения о состоянии объекта можно из него извлечь. Но, с другой стороны, если дли­тельность сигнала велика, то очень трудно обеспечить в течение этого вре­мени стабильность условий работы объекта и аппаратуры. При аналого-цифровом преобразовании сигнала оптимальная его длительность определя­ется из погрешности получения оцифрованного сигнала и разрешающей спо­собности по частоте. При этом необходимо задаться длиной выборки и пе­риодом дискретизации, которые определяют и ширину спектра сигнала. При многоканальных измерениях длина выборки будет определять время опроса датчиков. От длительности сигнала T зависит и время, необходимое для по­становки диагноза.

Требуемая полоса частот [ f_н, f_в ], в которой лежат спектры сигналов, излучаемых объектом при его различных состояниях, определяется главным образом длительностью соударений и частотной характеристикой канала, по которому сигналы проходят на первичный преобразователь. По различным причинам, спектр сигнала приходится искусственно ограничивать с помо­щью соответствующих фильтров. Существенно в период анализа модели объекта диагностирования правильно выбрать диапазон частот сигнала. При необоснованном расширении этого диапазона диагностическая аппаратура может быть в большой степени подвержена воздействию помех.

Итак, будем рассматривать класс сигналов фиксированной длительно­сти T, спектры которых лежат внутри фиксированного частотного диапазона [ f_н, f_в ]. Чтобы рассмотрению придать математический характер, прежде все­го, необходимо решить вопрос о математической форме представления сиг­нала. Эта задача решается теорией аппроксимации, в которой рассматрива­ются способы приближенного представления функций одного класса функ­циями другого класса.

Способ задания функции несущественен. Задача заключается в том, чтобы найти такую функцию F (t), которая была бы близка в определенном смысле к заданной функции s (t) и могла служить заменителем последней. Ограничим ее тем, что вместо произвольной функции F (t) будем для при­ближения использовать функции определенного класса, а именно многочлен вида

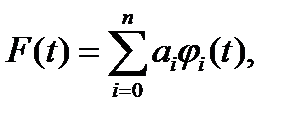                                                   (3.7)

где   a_i – постоянные коэффициенты; φ_i (t) – известные функции.

В качестве функций вида φ_i (t) целесообразно использовать функции, имеющие простую структуру, например, систему функций вида 1, t, t ²..., или 1, sin(ω ₁ t), cos(ω ₁ t), sin(2 ω ₁ t), cos(2 ω ₁ t),....

Задачу аппроксимации в нашем случае можно сформулировать в сле­дующем виде. Среди всех многочленов n -го порядка вида, (3.7), где φ_i (t) – известные функции, требуется найти такой многочлен, ко­торый был бы близок к заданной функции s (t). Для полной определенности этой формулировки необходимо уточнить, что понимают под близостью двух функций и что означает  «найти многочлен».

Для ответа на первый вопрос необходимо установить количественный критерий, который позволил бы оценивать сходство и различие между собой двух функций. Таких критериев существует несколько:

а) критерий равномерного приближения;

б) среднее отклонение как критерий близости функций;

в) среднеквадратичное отклонение как критерий близости функций.