III. Расчет температурных напряжений (охл)

Исходные данные.

 

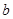
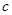
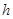
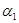
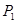
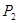
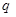
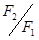
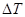
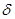
			d										Материал стержней
м	м	м	м	м			кН	кН	кН/м		oC	м
4	4	4	3	1	60	60	10	20	10	1			1. Медь
											-40	0,002	2. Al

Таблица 2

Справочные данные.

 

Материал стержней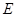
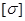
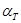
	МПа	МПа	oС-1
1. Медь		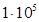100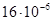
2. Al		60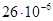

Задание:

Рассчитать площади поперечного сечения стержней конструкции.

Расчетная схема

 

 

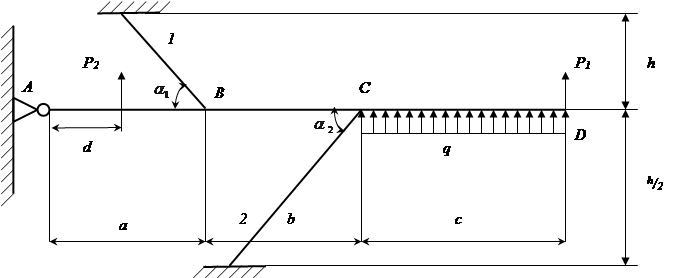Расчет усилий от внешних сил P₁; P₂ и сосредоточенной нагрузки q.

 

;

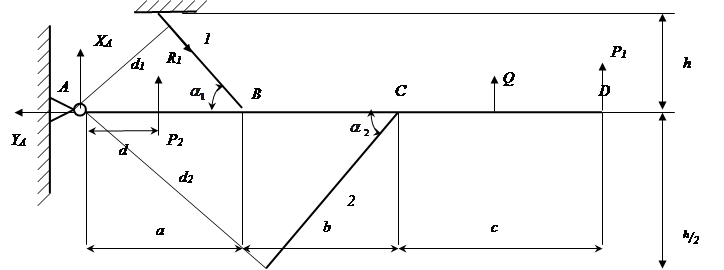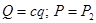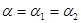
Определим, как повернется балка.

.

.

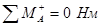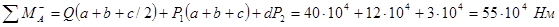Т.к. 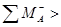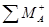, значит, балка повернется вверх (против часовой стрелки).

Составим уравнения статики:

;

(1.1)

или

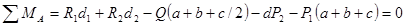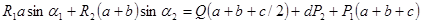
Таким образом, степень статической неопределимости системы 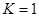, т.к. имеем два неизвестных усилия  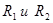и одно уравнение равновесия статики.

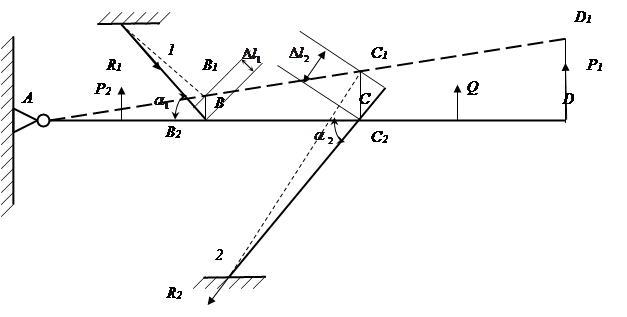Для составления условия совместимости деформации необходимо рассмотреть схему перемещений элементов системы.

 

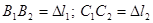
Составим условие совместности деформаций, используя подобие треугольников .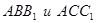

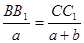
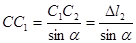
(1.2)

(1.3)

Откуда определим:

;

Подставив равенства (1.3) в формулу (1.2), получим условие совместности деформаций для заданной стержневой системы:

(1.4)

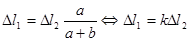
где 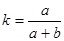 - безразмерный коэффициент, учитывающий особенности геометрической конфигурации системы.

Используя закон Гука для каждого из стержней, из уравнения (1.4) получим:

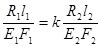
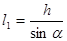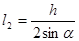Учитывая, что  и , последнее соотношение моно переписать следующим образом:

(1.5)

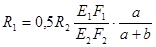
Далее решаем совместно систему уравнений (1.1) и (1.5):

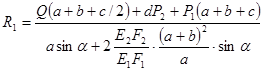
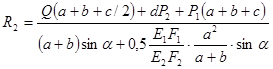
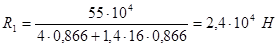
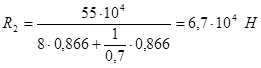
Проверка: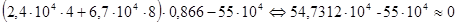

Погрешность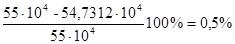

Так как первый стержень работает на сжатие, то окончательно принимаем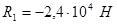

II. Определение напряжений, вызванных неточностью изготовления.

 

 

(2.1)

Уравнение равновесия для рассматриваемого случая будет иметь следующий вид:

(2.2)

Из схемы перемещений получим:

;

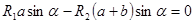
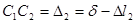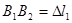
Составим условие совместности деформаций, используя подобие треугольников .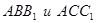

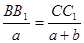
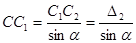
(2.3)

(2.4)

Откуда определим:

;

Подставив равенства (2.4) в формулу (2.3), получим условие совместности деформаций для заданной стержневой системы:

(2.5)

(2.6)

Подставим выражения (2.2) в равенство (2.5), получим условие совместимости деформаций:

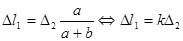
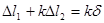
Используя закон Гука для каждого из стержней, из уравнения (2.6) получим:

(2.7)

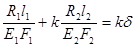
Перейдем в уравнении (2.7) к новым переменным, в качестве которых выберем монтажные напряжения

;

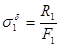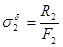
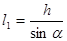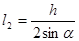Учитывая, что  и , последнее соотношение моно переписать следующим образом:

(2.8)

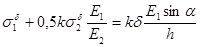
Перепишем уравнение (2.1) в напряжениях:

(2.9)

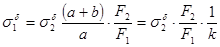
Решим систему уравнений (2.8) и (2.9) относительно неизвестных напряжений:

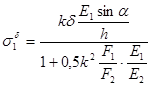
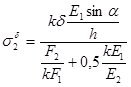
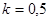
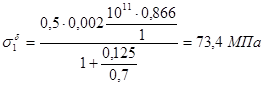
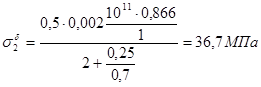
Проверка 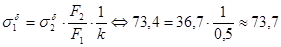 - верно

Так как оба стержня работают на сжатие, то окончательно принимаем 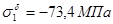 и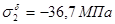

 

III.   Расчет температурных напряжений (охл).

 

 

(3.1)

Уравнение равновесия для рассматриваемого случая будет иметь следующий вид:

(3.2)

Из схемы перемещений получим:

;

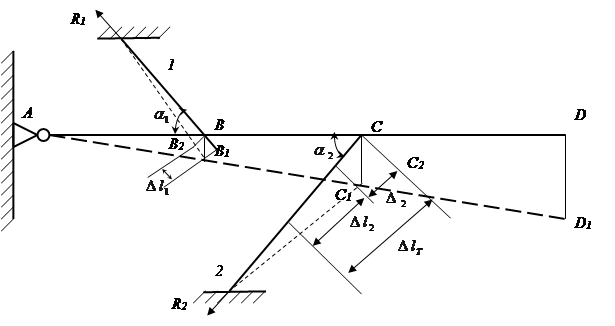
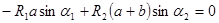
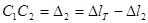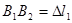
где .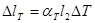

Составим условие совместности деформаций, используя подобие треугольников .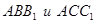

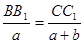
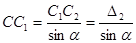
(3.3)

(3.4)

Откуда определим:

;

Подставив равенства (2.4) в формулу (2.3), получим условие совместности деформаций для заданной стержневой системы:

(3.5)

(3.6)

Подставим выражения (3.2) в равенство (3.5), получим условие совместимости деформаций:

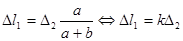
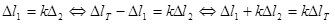
Используя закон Гука для каждого из стержней, из уравнения (3.6) получим:

(3.7)

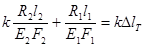
Перейдем в уравнении (3.7) к новым переменным, в качестве которых выберем монтажные напряжения

;

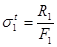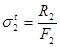
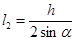Учитывая, что  и , последнее соотношение моно переписать следующим образом:

(3.8)

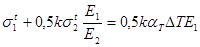
Перепишем уравнение (3.1) в напряжениях:

(3.9)

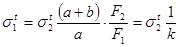
Решим систему уравнений (3.8) и (3.9) относительно неизвестных напряжений:

 

 

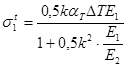
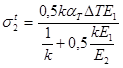
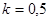
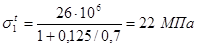
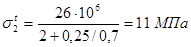
Проверка 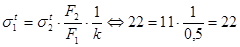 - верно