Анализ четырехполюсников и двухполюсников каскадной структуры с помощью матриц передачи

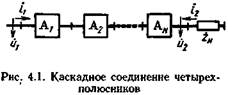
Многие четырехполюсные и двухполюсные устройства СВЧ имеют каскадную структуру, для которой характерно, что выход предшествующего четырехполюсника является входом последующего и т. д. (рис. 4.1). Анализ такого соединения значительно упрощается, если характеризовать четырехполюсники, а также их объединение специальными матрицами - матрицами передачи. При определении матриц передачи в качестве воздействия на четырехполюсник выбирается пара электрических величин, определяющих режим одного входа (обычно второго), а в качестве реакции - соответствующая пара величин, определяющая режим другого входа (обычно первого).

Для классической матрицы передачи 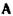 связь воздействия и реакции имеет вид

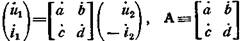 (4.1)

При таком определении матрица передачи любого числа каскадно включенных четырехполюсников оказывается равной произведению матриц передачи отдельных каскадов - это основное свойство любой матрицы передачи. Перемножать матрицы каскадов надо именно в той последовательности, в какой они включены в тракт.

Иногда предпочитают пользоваться так называемой волновой матрицей передачи, вводимой соотношениями

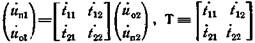
Каких-либо дополнительных возможностей по сравнению с матрицей 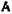 матрица  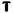не дает.

Из (4.1) следует, что элементы 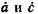 матрицы  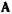представляют собой коэффициенты передачи по нормированному напряжению и нормированную взаимную проводимость при холостом ходе на выходе 2 четырехполюсника. Элементы  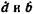- коэффициент передачи по нормированному току и нормированное взаимное сопротивление при коротком замыкании на выходе 2.

Зная элементы матрицы А, легко анализировать двухполюсники каскадной структуры, образующиеся при нагружении последнего каскада устройством с нормированным сопротивлением 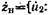 Входное сопротивление такого составного двухполюсника, согласно (4.1), будет 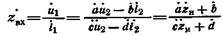  (4.2)

где использованы элементы матрицы .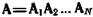

Если оконечная нагрузка представляет короткое замыкания или разрыв, то формула (4.2) упрощается и принимает одну из следующих форм: 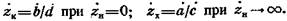 (4.3)

Коэффициент отражения составного двухполюсника можно найти по обычной формуле 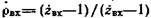, подставляя в нее значения  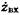из (4.2) или (4.3).