Введем пространство скоростей. Скорость 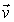 любой молекулы газа можно представить через её проекции
любой молекулы газа можно представить через её проекции 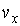 ,
, 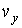 и
и 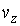 на соответствующие оси системы координат в пространстве скоростей. Если указанные значения отложить по осям
на соответствующие оси системы координат в пространстве скоростей. Если указанные значения отложить по осям 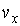 ,
, 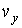 и
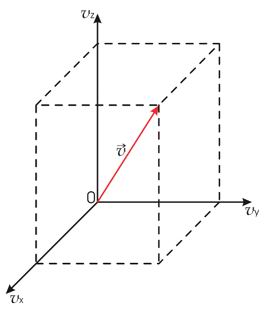
и 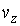 прямоугольной системы координат, то можно построить пространство скоростей, каждая точка в котором будет соответствовать определенному набору проекций скорости молекулы газа (см. рис. 5.3).
прямоугольной системы координат, то можно построить пространство скоростей, каждая точка в котором будет соответствовать определенному набору проекций скорости молекулы газа (см. рис. 5.3).
|
| Рис. 5.3. Пространство скоростей |
Далее сделаем предположение, что вероятности попадания значений проекций скорости молекулы 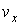 ,
, 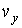 и
и 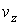 в соответствующие интервалы
в соответствующие интервалы 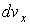 ,
, 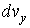 и
и 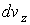 не зависят друг от друга, то есть значения проекций скорости молекул на ортогональные оси считаются статистически независимыми величинами. Тогда по аналогии с формулой
не зависят друг от друга, то есть значения проекций скорости молекул на ортогональные оси считаются статистически независимыми величинами. Тогда по аналогии с формулой 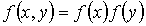 функцию распределения
функцию распределения 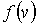 можно представить в виде:
можно представить в виде:
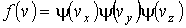 , ,
|
где 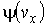 ,
, 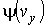 и
и 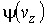 - функции распределения значений соответствующих проекций скорости
- функции распределения значений соответствующих проекций скорости 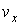 ,
, 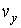 и
и 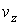 , причем вид этих функций должен быть одинаковым, так как все оси системы координат в пространстве скоростей равноправны.
, причем вид этих функций должен быть одинаковым, так как все оси системы координат в пространстве скоростей равноправны.
Прологарифмируем выражение 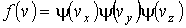 :
:
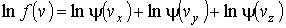 . .
|
Подстановка в него формулы, связывающей величину скорости и значения её проекций
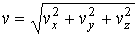 , ,
|
приводит к единственно возможному выражению для функции распределения:
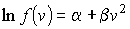
|
или
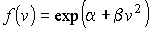 , ,
|
что полностью совпадает с формулой 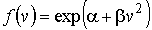 , полученной на основе применения принципа детального равновесия.
, полученной на основе применения принципа детального равновесия.
Соответственно функция распределения для значений проекций скорости 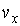 приобретает вид:
приобретает вид:
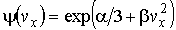 . .
|
Здесь константы 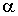 и
и 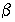 можно определять, исходя из условия нормировки
можно определять, исходя из условия нормировки  и значения среднего квадрата скорости хаотического движения молекул газа
и значения среднего квадрата скорости хаотического движения молекул газа 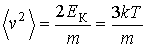 .
.
Введем следующие обозначения:
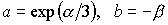 , ,
|
с учетом которых функция 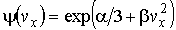 приобретет вид:
приобретет вид:
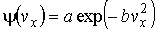 . .
|
В соответствии с условием нормировки  можно записать:
можно записать:
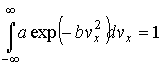 . .
|
Для нахождения интеграла 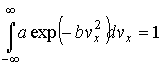 можно использовать интеграл Пуассона:
можно использовать интеграл Пуассона:
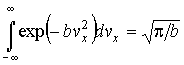 , ,
|
применение которого дает
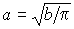 . .
|
Второе условие, которое может быть использовано для нахождения неизвестных констант, является следствием определения средней кинетической энергии молекул газа через его температуру 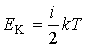 для случая одномерного движения:
для случая одномерного движения:
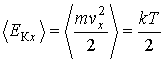 . .
|
Использование правила нахождения среднего значения 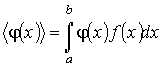 дает
дает
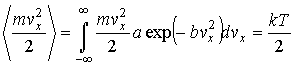 , ,
|
или с учетом формулы 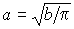
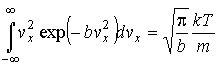 . .
|
Интеграл в выражении 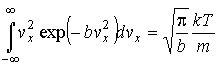 может быть проинтегрирован по частям с использованием интеграла Пуассона:
может быть проинтегрирован по частям с использованием интеграла Пуассона:
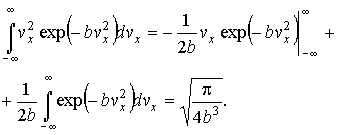
|
Подстановка получившегося выражения в 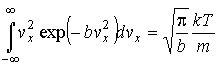 дает:
дает:
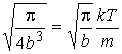 , ,
|
или
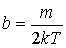 . .
|
Соответственно коэффициент 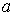 принимает вид
принимает вид
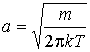 . .
|
Таким образом, функция 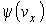 распределения значений проекции скорости
распределения значений проекции скорости 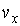 приобретает форму
приобретает форму
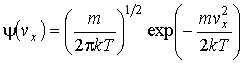 , ,
|
а функция распределения молекул газа по скоростям соответственно вид
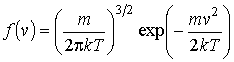
|
или
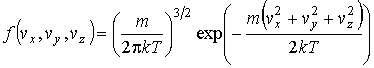 . .
|
Функции 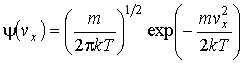 и
и 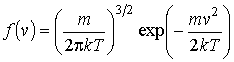
(или 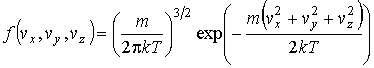 ) называются функциями распределения Максвелла. Качественно вид функции
) называются функциями распределения Максвелла. Качественно вид функции 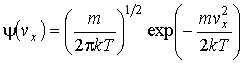 ,
,
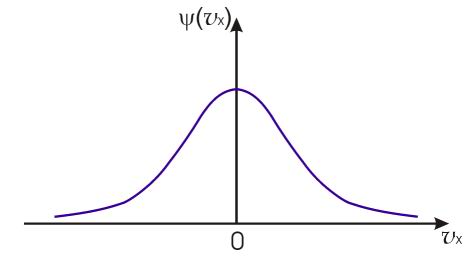
изображенной на рис. 5.4, совпадает с нормальным законом распределения Гаусса, описывающим распределение ошибок измерений случайной величины.
|
| Рис. 5.4. Распределение Максвелла |
Кроме полученного выше распределения Максвелла 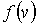 часто при проведении расчетов используется распределение по абсолютным значениям скоростей молекул газа. Для получения этого распределения запишем в общем виде вероятность того, что значения проекций скорости лежат внутри элементарного объема пространства скоростей
часто при проведении расчетов используется распределение по абсолютным значениям скоростей молекул газа. Для получения этого распределения запишем в общем виде вероятность того, что значения проекций скорости лежат внутри элементарного объема пространства скоростей  :
:
 . .
|
Учитывая то, что эта вероятность зависит только от величины скорости и не зависит от её направления в пространстве, элементарный объем 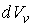 можно считать имеющим форму шарового слоя со средним радиусом
можно считать имеющим форму шарового слоя со средним радиусом 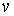 и толщиной
и толщиной 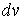 . Указанная возможность связана с тем, что в любой точке на поверхности сферы, центр которой совпадает с началом координат пространства скоростей, значения скорости
. Указанная возможность связана с тем, что в любой точке на поверхности сферы, центр которой совпадает с началом координат пространства скоростей, значения скорости 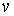 , а следовательно и функции
, а следовательно и функции  , одинаковые. Считая шаровой слой тонким, и записывая его элементарный объем в виде:
, одинаковые. Считая шаровой слой тонким, и записывая его элементарный объем в виде: 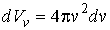 , выражение
, выражение  может быть представлено в форме
может быть представлено в форме
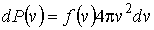 . .
|
Функция
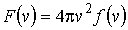
|
или
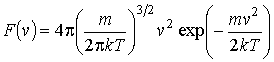
|
называется функцией распределения Максвелла по абсолютным значениям скоростей, и она показывает вероятность того, что величина скорости имеет значения от  до
до 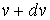 .
.
На рис. 5.5 изображен график функции распределения 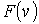 . Максимум этой функции соответствует наиболее вероятному значению скорости молекул газа
. Максимум этой функции соответствует наиболее вероятному значению скорости молекул газа 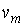 , которую можно определить, приравняв к нулю производную от функции
, которую можно определить, приравняв к нулю производную от функции 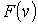 :
:
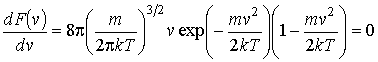 . .
|
Отсюда следует, что кроме случаев когда 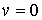 и
и 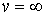 , соответствующих минимуму функции
, соответствующих минимуму функции 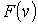 , имеется решение
, имеется решение
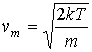 , ,
|
дающее выражение для наиболее вероятной скорости молекул газа.
|
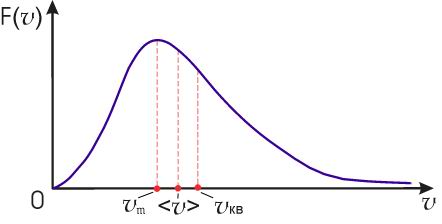
| Рис. 5.5. Распределение Максвелла по абсолютным значениям скоростей |
Кроме наиболее вероятной скорости, функция 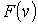 позволяет найти среднюю скорость
позволяет найти среднюю скорость
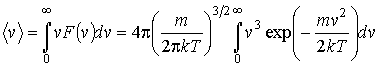
|
и среднее значение квадрата скорости
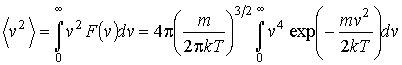 . .
|
Вычисление интегралов окончательно дает выражения для средней скорости
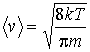
|
и для средней квадратичной скорости молекул
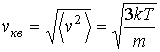 . .
|
Формула 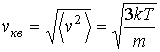 для средней квадратичной скорости может быть также получена на основании формулы
для средней квадратичной скорости может быть также получена на основании формулы 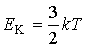 , описывающей среднюю кинетическую энергию поступательного движения молекул газа (см. вывод формулы
, описывающей среднюю кинетическую энергию поступательного движения молекул газа (см. вывод формулы 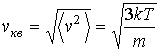 ).
).
Полученные значения скоростей численно отличаются друг от друга на величину, меньшую, чем их значения, причем  , что проиллюстрировано на рис. 5.5.
, что проиллюстрировано на рис. 5.5.
Кроме функции распределения по абсолютным значениям скорости 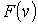 применяется функция распределения по значениям кинетической энергии поступательного движения молекул
применяется функция распределения по значениям кинетической энергии поступательного движения молекул 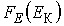 , характеризующая вероятность попадания значений кинетической энергии
, характеризующая вероятность попадания значений кинетической энергии 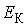 в интервал
в интервал 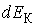 :
:
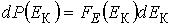 . .
|
Приравняв вероятности 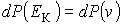 или
или 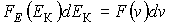 , и используя подстановку
, и используя подстановку 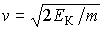 и
и 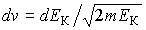 , имеем:
, имеем:
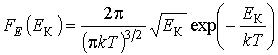 . .
|
 2020-07-12
2020-07-12 112
112








