2020-07-12
98
Так как при адиабатических процессах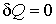 
, то первое начало термодинамики для них можно записать в форме:
 .
|
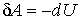Совместное применение этого выражения и уравнения Клапейрона-Менделеева позволяет получить уравнение, описывающее адиабатический процесс в идеальном газе. Для этого представим выражение 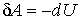в виде:
 .
|
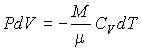Нахождение полных дифференциалов от правой и левой частей уравнения Клапейрона-Менделеева 
дает:
 .
|
Вычитание из этой формулы выражения 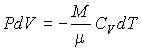. Приводит его к виду
 .
|
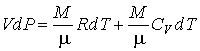С учетом соотношения Майера 
имеем:
 .
|
Умножим выражение 
. на отношение теплоемкостей 
и сложим его с формулой 
.. Тогда получим
 ,
|
где введено обозначение
 .
|
Величина 
называется показателем адиабаты. Формулы 
и 
позволяют определить показатель адиабаты через количество степеней свободы 
:
 .
|
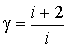Из этого выражения следует, что показатель адиабаты для идеального газа всегда больше единицы. Для одноатомных газов этот показатель равен 1,67, а для двухатомных и многоатомных соответственно 1,4 и 1,33.
|
|
|
Поделив уравнение на произведение 
преобразуем его к виду
|
или
 .
|
Отсюда следует:
 .
|
Интегрирование этого уравнения позволяет получить формулу
 .
|
которая называется уравнением Пуассона. Это уравнение адиабатического процесса для идеального газа, или адиабаты - кривой, описываемой этим уравнением в переменных 
и 
.
