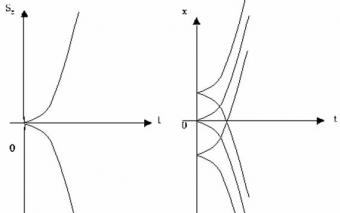
| Равнопеременное движение. Ускорение. | |
| Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением. | |
Обозначим:  - вектор начальной скорости, - вектор начальной скорости, 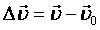 - изменение скорости, а Δt - промежуток времени.
Пусть Δt1= Δt2=Δt3=..., тогда по определению - изменение скорости, а Δt - промежуток времени.
Пусть Δt1= Δt2=Δt3=..., тогда по определению 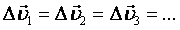
| |
Следовательно, 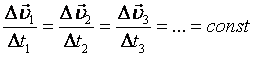 Т.о., это характеристика движения.
Т.о., это характеристика движения.
| |
Если t0=0, то 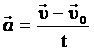
| 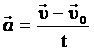
|
| УСКОРЕНИЕ - физическая величина, характеризующая быстроту изменения скорости и (при равнопеременном движении) численно равная отношению вектора изменения скорости к промежутку времени, в течение которого это изменение произошло. | |
| Ускорение при равнопеременном движении показывает, насколько меняется мгновенная скорость движения тела за единицу времени. Единица ускорения в СИ - м/с2. | Например, ускорение равно 5 м/с2 - это значит, что, двигаясь равноускоренно, тело изменяет скорость на 5 м/с за каждую секунду своего движения. |
В случае не равнопеременного движения: 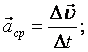 тогда мгновенное ускорение
тогда мгновенное ускорение 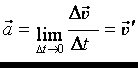
| |
| Равнопеременное движение называется равноускоренным, если модуль скорости возрастает. | Условие р.у.д. - 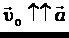 . .
|
| Равнопеременное движение называется равнозамедленным, если модуль скорости уменьшается. | Условие р.з.д. -  . .
|
| Графики равнопеременного движения. | |
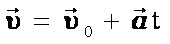
| 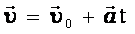
|
или 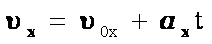 - в проекциях;
или - в проекциях;
или 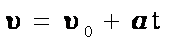 – через модули. – через модули.
| 
|
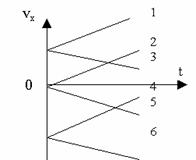
| Линейная функция. График - прямая. | |
Движения, совпадающие с направлением координатной оси:
| 
|
| Перемещение при равнопеременном движении. | |
| Площадь под графиком скорости численно равна перемещению. Следовательно, площадь трапеции численно равна перемещению. | 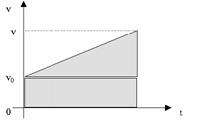
|
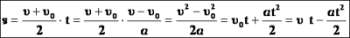
| Решение основной задачи механики для р.у.д.:
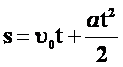 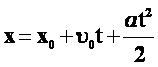
|
| Графики перемещения и координаты. | |
| Функции | |
|
| |
 2020-08-05
2020-08-05 204
204