Добавление точки Р и -P

Линия, проходящая через Р и -Р представляет собой вертикальную линию, которая не пересекает эллиптической кривой на третьей точке; Таким образом, точки P и -P не могут быть добавлены, как ранее. Именно по этой причине, что эллиптическая кривая группа включает в себя бесконечно удаленную точку O. По определению, Р + (-P) = О.

Выведем формулы для определения координат результирующей точки 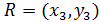на основе координат исходных точек и Рассмотрим вначале случай, когда 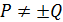(рис. 6.4). Обозначим через k угловой коэффициент прямой, проходящей через P и Q. Очевидно, что

Тогда уравнение прямой будет иметь вид , откуда

Подставим найденное выражение дли переменной Y в уравнение кривой (6.1). Получим

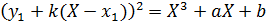
Возводя в квадрат и группируя подобные члены, получим кубическое уравнение

Известно, что сумма корней кубического уравнения равна коэффициенту при X², взятому с противоположным знаком (теорема Виета для кубических уравнений), т.е.

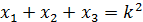
откуда

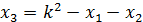
Подставив найденное значение х₃ в уравнение прямой (6.6), найдем ординату точки , и, изменив знак, получим

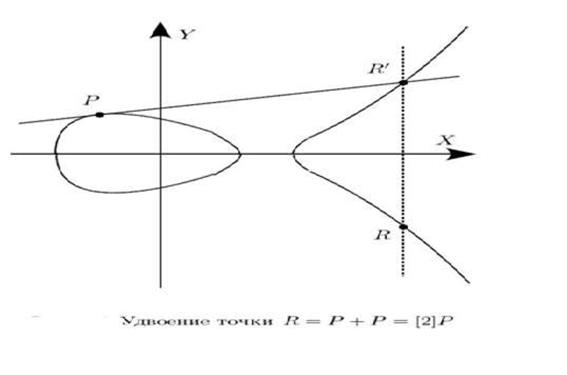
Теперь рассмотрим случай, когда Р = Q и результирующая точка R = [2] Р (рис. 6.5). Дифференцируя обе части (6.1) но X, получим

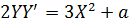
Угловой коэффициент касательной равен значению производной в точке P,

Дальнейшее рассуждение аналогично первому случаю, и координа-

Используя полученные формулы для вычисления композиции и принятые соглашения относительно точки в бесконечности, можно доказать следующие свойства точек на эллиптической кривой:

1) P + Q = Q + P для всех точек ;

2) Р + (Q + S) = (Р + Q) + S для всех точек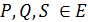

3) существует нулевой элемент О (точка в бесконечности), такой, что P + O = О + Р = Р для всех ;

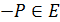4) для каждой точки существует точка , такая, что Р + (—Р) = О.

Перечисленные свойства точек совпадают со свойствами целых чисел при использовании операции сложения. Поэтому композицию точек часто называют сложением точек, а операцию [2]Р удвоением точки.

Продолжая аналогию со сложением чисел, удобно ввести следующие обозначения. Для целого m

Теперь мы готовы к тому, чтобы сделать последний шаг, необходимый для криптографического использования эллиптических кривых. Мы видим, что при вычислении композиции точек на кривой (см. формулы (6.5), (6.9), (6.7) и (6.8)) используются только операции сложения, вычитания, умножения и деления чисел. Это значит, что все приведенные выше тождества сохранятся, если мы будем выполнять вычисления с целыми числами по модулю простого числа р. В этом случае сложение и умножение чисел выполняются по модулю р, разность u - v вычисляется как u + (р — v) mod р, а деление u/v выполняется путем умножения u на v^-1 mod р (простота модуля гарантирует. что для любого положительного числа v < р существует число v^-1, такое, что vv^-^l mod р = 1).

В результате мы получаем кривую

В уравнении (6.10) переменные X, Y и коэффициенты а, b принимают целочисленные значения, а все вычисления выполняются по модулю р. В соответствии с (6.4) на а, b налагается ограничение

Множество Е_р(а, b) состоит из всех точек (х, у), 0 < х, у < р, удовлетворяющих уравнению (6.10), и точки в бесконечности О. Количество точек в Е_р (а, b) будем обозначать #Е_р(a, b). Эта величина имеет важное значение для криптографических приложений эллиптических кривых.

Пример 6.1. Рассмотрим кривую

Проверим условие (6.11):

Итак, данная кривая несингулярна. Найдем какую-нибудь (случайную) толку в Е₇(2, 6). Пусть х = 5. Тогда

и y = 1 (mod 7) или y = -1 =6 (mod 7). Мы нашли сразу две точки: (5, 1) и (5, 6). Найдем еще пару точек путем вычисления композиции. Вначале найдем [2] (5, 1). Используя (6, 9), (6, 7) и (6, 8), вычисляем

Мы получили [3](5, 1) = (2, 5). Итак, мы нашли четыре точки. Для криптографического использования кривой важно знать, сколько всего точек в множестве E₇(2, 6).

Скажем несколько слов о свойствах множества точек Е_р(а, b). Очевидно, что это множество конечно, так как в него входят только точки с целочисленными координатами О < x, у < р. Существует прямая аналогия между' Е_р (а, b) и множеством степеней целых чисел, вычисляемых по модулю р. Так, Е_р (а, b) имеет генератор, т.е. такую точку G. что ряд G. [2] G, [3]G, …, [n]G, где n = #Е_р(а, b), содержит все точки множества Е_р(а, b), причем [n]G = О (аналогично «действовал» параметр g в разд. 2.2). Число точек на кривой, при надлежащем выборе параметров р, а и b, может быть простым числом, #Е_р (а, b) = q. В этом случае любая точка (кроме О) является генератором всего множества точек. Такая кривая предпочтительна во многих отношениях и всегда может быть найдена за практически приемлемое время. Если по каким-то причинам такую кривую найти не удалось и #Е_р (а, b) = hq, где q — опять простое число, то в Е_р (а, b) существует подмножество из q точек (т.е. мощности q), генератором которого может служить любая точка G ≠ О, такая что [q]G = О. В дальнейшем, без потери общности, мы будем считать, что работаем с таким подмножеством мощности q (а при выборе кривой будем стремиться получить q = #Е_р (а, b)).

Основная криптографическая операция на эллиптической кривой m-кратная композиция, т.е. вычисление

Q = [m}P = P + P +…+Р. (6.13)

Эта операция выполняется очень эффективно и требует не более 2 log m композиций точек. Подходы к ее реализации абсолютно те же, что и к возведению в степень. Например, чтобы получить точку Q = [21] Р, вычисляем [2]Р, [4 Р, [8]Р, [16]Р, каждый раз удваивая предыдущую точку, и складываем Р + [4]Р + [16]Р = Q (всего 4 удвоения и 2 сложения).

Обратная задача, которая по традиции называется дискретным логарифмированием на эллиптической кривой, формулируется следующим образом. Зная точки Р и Q, найти такое число т, что [m]Р = Q. Эта задача оказывается очень трудной. Если тщательно выбрать параметры кривой (как описывается в следующем разделе), то наилучшие известные в настоящее время алгоритмы для нахождения т требуют операций на кривой, где q — мощность подмножества точек, которому принадлежат точки Р и Q. Все вычисления на кривой проводятся по модулю р, т.е. с числами длины 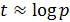бит. Для криптографических приложений поэтому 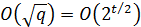означает экспоненциальный рост трудоемкости при увеличении длины чисел.