Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:
 (14)
(14)
Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведение второй на производную первой, т. е.
 .
.
Следствие. Постоянный множитель можно выносить за знак производной 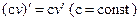 .
.
Производная частного двух дифференцируемых функций определяется формулой
 .
.
Производная сложной функции. Если y = f(u) и u = φ(x) – дифференцируемые функции своих аргументов, то производная сложной функции y=f(φ(x)) существует и равна производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т. е.
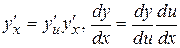 . (15)
. (15)
Производная обратной функции. Если y = f(x) и x = φ(y) – взаимно обратные дифференцируемые функции и  , то
, то
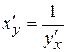 .
.
Если функция 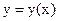 задана параметрически, то есть уравнениями
задана параметрически, то есть уравнениями
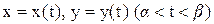 , где
, где 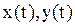 – дифференцируемые функции и
– дифференцируемые функции и  то её производная
то её производная  определяется формулой
определяется формулой

Основные формулы дифференцирования. Если 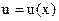 – дифференцируемая функция, то:
– дифференцируемая функция, то:
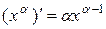 ; (16)
; (16)
 (17)
(17)

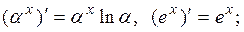 (18)
(18)
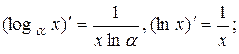 (19)
(19)
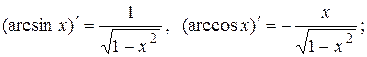
 (20)
(20)
Пример 22. Найти производную функции 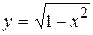 .
.
Решение. Считая  и применяя формулу (16), получаем
и применяя формулу (16), получаем
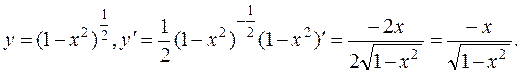
Пример 23. Найти производную функции  .
.
Решение. Применяя формулу (17), находим

Пример 24. Найти производную функции 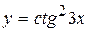 .
.
Решение. Применяем формулу (15), находим

Пример 25. Найти производную функции  .
.
Решение. Так как  ,
, 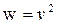 ,
, 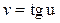 ,
,  , то по формуле
, то по формуле
(15) получаем  ,
,
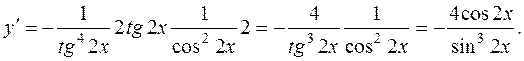
Пример 26. Найти производную функции 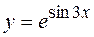 .
.
Решение. Применяя формулы (15) и (18), находим

Пример 27. Найти производную функции 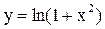 .
.
Решение. На основании формул (15), (19), (14) получаем
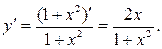
Пример 28. Найти производную функцию, заданную уравнением 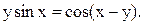
Решение. Это уравнение определяет функцию 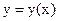 от
от 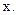 Подставляя функцию
Подставляя функцию  в данное уравнение, получаем тождество
в данное уравнение, получаем тождество 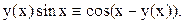
Дифференцируем это тождество и из полученного уравнения находим 
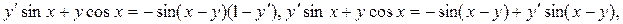
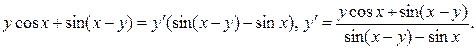
Пример 29. Найти производную функцию, заданную уравнениями 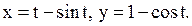
Решение. Эта функция задана параметрически. Так как 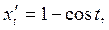
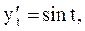 то по формуле (10) получаем
то по формуле (10) получаем 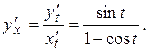
Пример 30. Найти производную функции 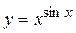 .
.
Решение. Логарифмируя это равенство по основанию е, получаем  Дифференцируя, находим
Дифференцируя, находим  откуда
откуда 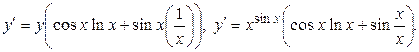
Дифференциал функции. Если приращение функции представимо в виде
Dу = АDх+ о (Dх),
где А – постоянная, о (Dх) – бесконечно малая высшего порядка по сравнению с Dх, то слагаемое АDх называют дифференциалом функции f(x) в точке х0 и обозначают dy; функцию в этом случае называют дифференцируемой в точке х0.
Так как dx = Dх, то dy = f ¢ (х)dx.
Дифференциалы и производные высших порядков. Производной n – го порядка f n (x) называется производная от производной (n - 1) – го порядка. Дифференциалом n – го порядка d n y называется дифференциал от дифференциала (n-1) – го порядка как функции х:
d n y = d (d n-1 y).
Правило Лопиталя – Бернулли. Если функции f(x) и φ(x), дифференцируемые в окрестности точки x=a обращаются в нуль и существует предел отношения f´(x)/φ´(x) при x→a, то существует предел отношения самих функций и
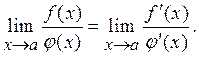
Замечание. Если f´(a) = 0, φ´(a) = 0, функции f´(x), φ´(x) дифференцируемы в окрестности точки x=a и существует предел отношения f´´(x)/φ´´(x) при x→а, то
 .
.
С помощью тождественных преобразований к основному виду  или
или 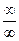 можно свести неопределённости других видов, таких, как
можно свести неопределённости других видов, таких, как 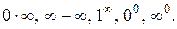
Пример 31. Найти 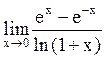 .
.
Решение. При 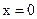 числитель и знаменатель дроби обращаются в нуль, имеем неопределённость вида
числитель и знаменатель дроби обращаются в нуль, имеем неопределённость вида 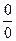 . Чтобы раскрыть её, применяем правило Лопиталя-Бернулли:
. Чтобы раскрыть её, применяем правило Лопиталя-Бернулли:
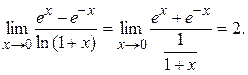
Пример 32. Найти 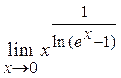 .
.
Решение. При  получаем неопределённость вида
получаем неопределённость вида 
Обозначим  и прологарифмируем это равенство по основанию е:
и прологарифмируем это равенство по основанию е:
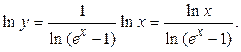
В правой части этого равенства при 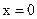 имеем неопределённость вида
имеем неопределённость вида 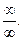 Применяя дважды правило Лопиталя-Бернулли, находим
Применяя дважды правило Лопиталя-Бернулли, находим

Следовательно, 
 2020-08-05
2020-08-05 89
89








