Пример 1. Найдите все значения параметра a, для каждого из которых при любом значении параметра b уравнение имеет ровно два корня.
x 2 − 4| x |− 7| b − a | + 3| b − 3|− 2 b + 5 a − 15 = 0
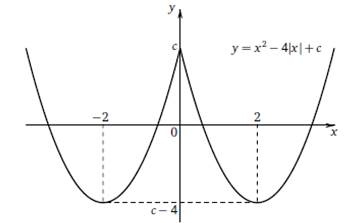
Решение. Обозначим выражение −7| b − a | + 3| b −3| − 2 b + 5 a −15 через c и рассмотрим график чётной функции y = x 2 − 4| x |+ c, состоящий из двух частей парабол y = x 2 − 4 x + c (при x ≥0) и
y = x 2 + 4 x + c (при x <0) с вершинами в точках (2; c −4) и (−2; c − 4) соответственно.
Действительно, х вершины = - b/2 = - (- 4)/2 = 2; у = 4 – 8 + с = с – 4.
При c <0 график пересекает ось абсцисс в двух точках; при c = 0 в трёх точках, при 0 < c <4 - в четырёх точках; при c = 4 - в двух точках; при c > 4 график не имеет с осью абсцисс ни одной общей точки (смотри рисунок).
Данное уравнение имеет ровно два корня, если график пересекает ось абсцисс в двух точках, т. е. если c = 4 или c <0. Рассмотрим оба этих случая.
Пусть c = 4, т. е. −7| b − a | + 3| b − 3| − 2 b + 5 a − 15 = 4, откуда
7| b − a | − 3| b − 3| + 2 b − 5 a + 19 = 0.
Последнее равенство должно выполняться при любом значении b, в частности при b = 3 (так, чтобы| b − 3|= 0). В этом случае получаем 7|3 − a | + 6 − 5 a + 19 = 0, или 7| a − 3| = 5 a − 25.
В силу неотрицательности модуля корни последнего уравнения должны удовлетворять неравенству 5 a − 25 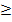 0, т. е. неравенству a
0, т. е. неравенству a 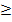 5. Но тогда 7 a – 21 = 5 a − 25 и a = −2 либо
5. Но тогда 7 a – 21 = 5 a − 25 и a = −2 либо
7 a – 21 = 25 − 5 a и a = 23/6.
Ни одно из найденных значений a не удовлетворяет неравенству a 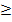 5.
5.
Следовательно, в этом случае решений нет.
Пусть c <0, т. е. −7| b − a | + 3| b −3|−2 b + 5 a − 15<0. Обозначим g (b) = −7| b − a |+3| b −3|−2 b + 5 a −15. График непрерывной функции y = g (b) представляет собой ломаную, состоящую из отрезков
прямых и лучей. При b >a каждое звено ломаной является частью прямой вида y = kb + l, где k <0.
Докажем это утверждение. Если b ≥ 3, то g (b) = −7(b – a) + 3(b −3) − 2 b + 5 a −15 = −7 b +7 a + 3 b – 9 −2 b + 5 a −15 = - 6 b + (12 a – 24). Если b < 0, то g (b) = −7 b + 7 a + 9 - 3 b − 2 b + 5 a −15 = − 12 b +(12 a – 6).
Следовательно, при b > a функция y = g (b) убывает.
Совершенно аналогично докажем, что при b < a функция y = g (b) возрастает. При b < a каждое звено ломаной является частью прямой вида y = kb + l, где k > 0.
Докажем это утверждение. Если b ≥ 3, то g (b) = −7(a - b) + 3(b −3) − 2 b + 5 a −15 = −7 a +7 b + 3 b – 9 −2 b + 5 a −15 = 8 b + (-2 a – 24). Если b < 0, то g (b) = −7 a + 7 b + 9 - 3 b − 2 b + 5 a −15 = 2 b +(-2 a – 6).
Следовательно, при b < a функция y = g (b) возрастает.
Поэтому в точке b = a эта функция достигает своего наибольшего значения, т. е. max g (b) = g (a). Поэтому неравенство −7| b − a | + 3| b − 3| − 2 b + 5 a − 15 < 0 будет выполняться при любом
значении b в том и только том случае, если max g (b) < 0, т. е. если g (a) < 0.
Но g (a) = 3| a − 3| + 3 a − 15. Остаётся решить неравенство 3| a −3|+ 3 a −15 < 0. Преобразуем неравенство к виду | a −3| < 5− a и перейдём к системе
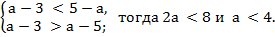
Второе неравенство системы выполняется при любом значении a
Ответ: (−∞; 4).
Задания для самостоятельного решения
1. Найдите все значения параметра a, для каждого из которых при любом значении параметра b уравнение имеет ровно два корня.
x 2− 4| x |−7| a + b + 1|+3| b − 1|− 2 b − 5 a − 14 = 0
2 Найдите все значения параметра a, для каждого из которых при любом значении параметра b уравнение имеет ровно два корня.
x 2− 4| x |− 7| a + 2 b − 1|+3|2 b + 3|− 4 b + 5 a − 20 = 0
 2020-08-05
2020-08-05 393
393








