КОЖНЕ ЗАВДАННЯ СКЛАДАЄТЬСЯ З 30 ВАРІАНТІВ.
Завдання № 1
Який з поданих функціональних рядів є степеневим?
1.1. а) 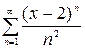 , б)
, б) 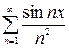 , в)
, в)  , г)
, г) 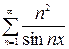 .
.
1.2. а)  , б)
, б)  , в)
, в)  , г)
, г) 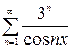 .
.
1.3. а) 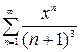 , б)
, б) 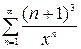 , в)
, в)  , г)
, г) 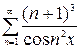 .
.
1.4. а) 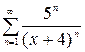 , б)
, б)  , в)
, в) 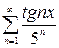 , г)
, г) 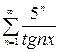 .
.
1.5. а)  , б)
, б)  , в)
, в) 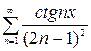 , г)
, г) 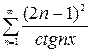 .
.
1.6. а) 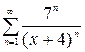 , б)
, б) 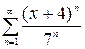 , в)
, в)  , г)
, г) 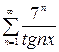 .
.
1.7. а) 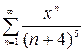 , б)
, б) 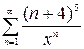 , в)
, в) 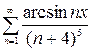 , г)
, г) 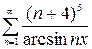 .
.
1.8. а) 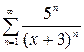 , б)
, б)  , в)
, в)  , г)
, г) 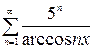 .
.
1.9. а) 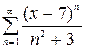 , б)
, б) 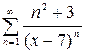 , в)
, в) 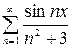 , г)
, г)  .
.
1.10. а) 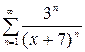 , б)
, б)  , в)
, в) 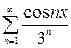 , г)
, г) 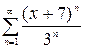 .
.
1.11. а)  , б)
, б)  , в)
, в) 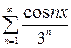 , г)
, г) 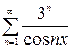 .
.
1.12. а) 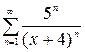 , б)
, б)  , в)
, в) 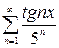 , г)
, г) 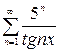 .
.
1.13. а) 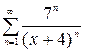 , б)
, б) 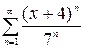 , в)
, в)  , г)
, г)  .
.
1.14. а) 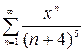 , б)
, б) 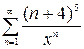 , в)
, в)  , г)
, г)  .
.
1.15. а) 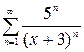 , б)
, б)  , в)
, в) 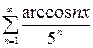 , г)
, г) 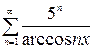 .
.
1.16. а)  , б)
, б) 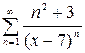 , в)
, в)  , г)
, г) 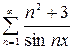 .
.
1.17. а) 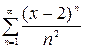 , б)
, б) 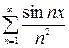 , в)
, в) 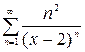 , г)
, г) 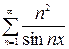 .
.
1.18. а) 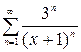 , б)
, б) 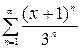 , в)
, в)  , г)
, г) 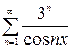 .
.
1.19. а) 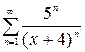 , б)
, б)  , в)
, в) 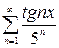 , г)
, г) 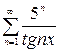 .
.
1.20. а) 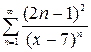 , б)
, б) 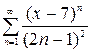 , в)
, в) 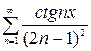 , г)
, г) 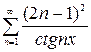 .
.
1.21. а)  , б)
, б) 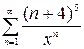 , в)
, в) 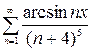 , г)
, г) 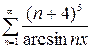 .
.
1.22. а) 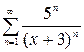 , б)
, б) 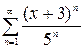 , в)
, в) 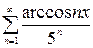 , г)
, г) 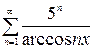 .
.
1.23. а) 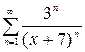 , б)
, б) 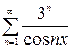 , в)
, в) 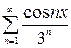 , г)
, г) 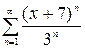 .
.
1.24. а)  , б)
, б) 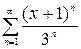 , в)
, в) 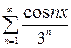 , г)
, г) 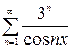 .
.
1.25. а) 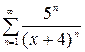 , б)
, б)  , в)
, в) 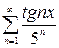 , г)
, г) 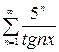 .
.
1.26. а) 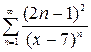 , б)
, б) 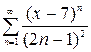 , в)
, в) 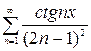 , г)
, г) 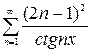 .
.
1.27. а) 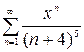 , б)
, б) 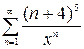 , в)
, в) 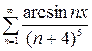 , г)
, г)  .
.
1.28. а) 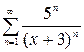 , б)
, б)  , в)
, в) 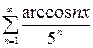 , г)
, г) 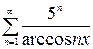 .
.
1.29. а) 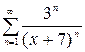 , б)
, б)  , в)
, в) 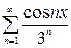 , г)
, г)  .
.
1.30. а) 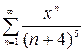 , б)
, б) 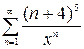 , в)
, в)  , г)
, г) 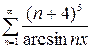 .
.
Завдання № 2
Для даного ряду знайти центр інтервалу збіжності, радіус інтервалу збіжності та дослідити поводження ряду в граничних точках і знайти область збіжності.
2.1. 
| 2.16. 
|
2.2. 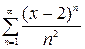
| 2.17. 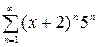
|
2.3. 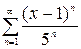 . .
| 2.18. 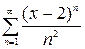
|
2.4. 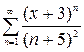
| 2.19. 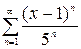 . .
|
2.5. 
| 2.20. 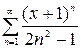
|
2.6. 
| 2.21. 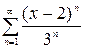
|
2.7. 
| 2.22. 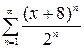
|
2.8. 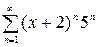
| 2.23. 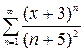
|
2.9. 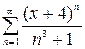
| 2.24. 
|
2.10. 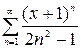
| 2.25. 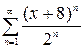
|
2.11. 
| 2.26. 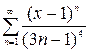
|
2.12. 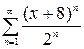
| 2.27. 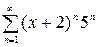
|
2.13. 
| 2.28. 
|
2.14. 
| 2.9. 
|
2.15. 
| 2.30. 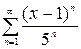 . .
|
Завдання № 3
Знайти коефіцієнт при 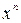 в розкладанні даної функції в ряд Маклорена.
в розкладанні даної функції в ряд Маклорена.
3.1.  2, 2, 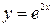
| 3.16.  1, 1, 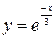
|
3.2.  3, 3, 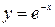
| 3.17.  2, 2, 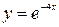
|
3.3.  3, 3, 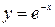
| 3.18.  3, 3, 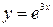
|
3.4.  3, 3, 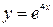
| 3.19.  1, 1, 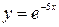
|
3.5.  3, 3, 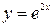
| 3.20.  2, 2, 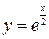
|
3.6.  2, 2, 
| 3.21.  2, 2, 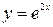
|
3.7.  1, 1, 
| 3.22.  1, 1, 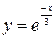
|
3.8.  2, 2, 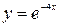
| 3.23.  3, 3, 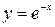
|
3.9. 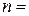 3, 3, 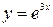
| 3.24. 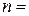 3, 3, 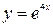
|
3.10. 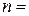 1, 1, 
| 3.25. 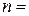 3, 3, 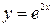
|
3.11.  2, 2, 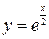
| 3.26.  2, 2, 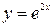
|
3.12.  1, 1, 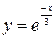
| 3.27.  3, 3, 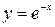
|
3.13.  2, 2, 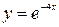
| 3.28.  3, 3, 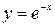
|
3.14.  3, 3, 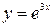
| 3.29.  3, 3, 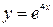
|
3.15.  1, 1, 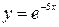
| 3.30.  3, 3, 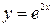
|
Завдання № 4
Обчислити дану функцію, використовуючи два члени ряду та знайти
погрішність обчислювань 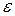 .
.
4.1. 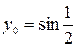
| 4.16. 
|
4.2. 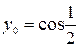
| 4.17. 
|
4.3. 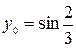
| 4.18. 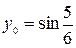
|
4.4. 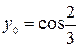
| 4.19. 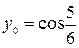
|
4.5. 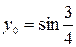
| 4.20. 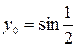
|
4.6. 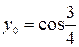
| 4.21. 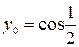
|
4.7. 
| 4.22. 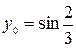
|
4.8. 
| 4.23. 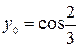
|
4.9. 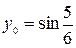
| 4.24. 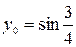
|
4.10. 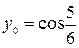
| 4.25. 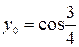
|
4.11. 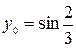
| 4.26. 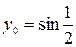
|
4.12. 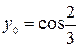
| 4.27. 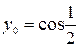
|
4.13. 
| 4.28. 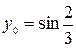
|
4.14. 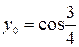
| 4.29. 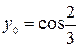
|
4.15. 
| 4.30. 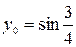
|
Завдання № 5
Обчислити дану функцію з точністю 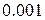
5.1. 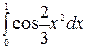
| 5.16. 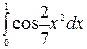
|
5.2. 
| 5.17. 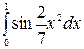
|
5.3. 
| 5.18. 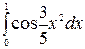
|
5.4. 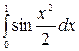
| 5.19. 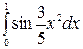
|
5.5. 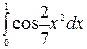
| 5.20. 
|
5.6. 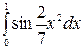
| 5.21. 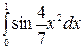
|
5.7. 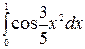
| 5.22. 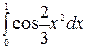
|
5.8. 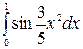
| 5.23. 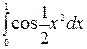
|
5.9. 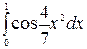
| 5.24. 
|
5.10. 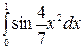
| 5.25. 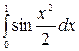
|
5.11. 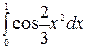
| 5.26. 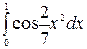
|
5.12. 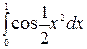
| 5.27. 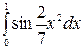
|
5.13. 
| 5.28. 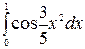
|
5.14. 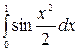
| 5.29. 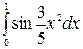
|
5.15. 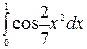
| 5.30. 
|
Завдання № 6
Знайти розкладання в степеневий ряд по ступенях 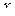 рішення даного диференційного рівняння з початковими умовами (три перших члени розкладання, що відрізняються від нуля)
рішення даного диференційного рівняння з початковими умовами (три перших члени розкладання, що відрізняються від нуля)
6.1. 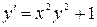 , , 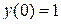
| 6.16. 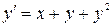 , , 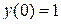
|
6.2. 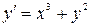 , , 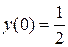
| 6.17.  , , 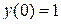
|
6.3. 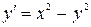 , , 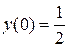
| 6.18.  , , 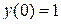
|
6.4. 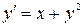 , , 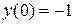
| 6.19. 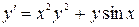 , , 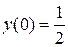
|
6.5. 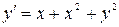 , , 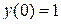
| 6.20. 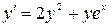 , , 
|
6.6.  , , 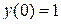
| 6.21. 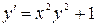 , , 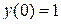
|
6.7.  , , 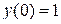
| 6.22. 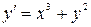 , , 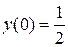
|
6.8. 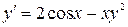 , , 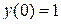
| 6.23. 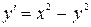 , , 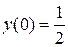
|
6.9.  , , 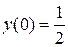
| 6.24. 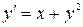 , , 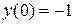
|
6.10. 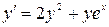 , , 
| 6.25. 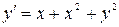 , , 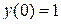
|
6.11.  , , 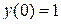
| 6.26. 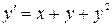 , , 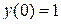
|
6.12. 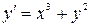 , , 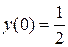
| 6.27.  , , 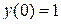
|
6.13. 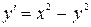 , , 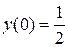
| 6.28. 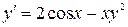 , , 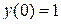
|
6.14. 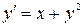 , , 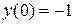
| 6.29.  , , 
|
6.15. 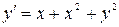 , , 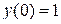
| 6.30. 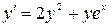 , , 
|
Завдання № 7
Розкласти в ряд Фур’є дану функцію, що задана на інтервалі 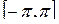
7.1. 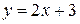
| 7.16. 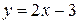
|
7.2. 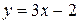
| 7.17. 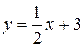
|
7.3. 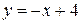
| 7.18. 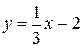
|
7.4. 
| 7.19. 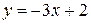
|
7.5. 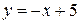
| 7.20. 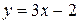
|
7.6. 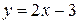
| 7.21. 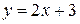
|
7.7. 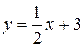
| 7.22. 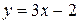
|
7.8. 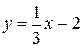
| 7.23. 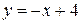
|
7.9. 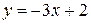
| 7.24. 
|
7.10. 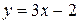
| 7.25. 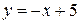
|
7.11. 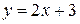
| 7.26. 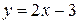
|
7.12. 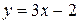
| 7.27. 
|
7.13. 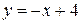
| 7.28. 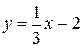
|
7.14. 
| 7.29. 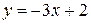
|
7.15. 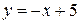
| 7.30. 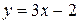
|
Анотація до АКР
Контрольна робота (тест) включає практичні та теоретичні питання по розділу „Степеневі ряди і ряди Фур'є”.
Тест містить сім завдань. Критерій оцінювання знань студентів визначається ваговим коефіцієнтом цих завдань:
| № завдання | Коефіцієнт |
| 1 | 0,03 |
| 2 | 0,14 |
| 3 | 0,07 |
| 4 | 0,1 |
| 5 | 0,21 |
| 6 | 0,19 |
| 7 | 0,26 |
Всі завдання мають чотири варіанти відповідей, серед яких є одна вірна.
Завдання № 1 перевіряє знання студентами загальної форми запису степеневого ряду.
Завдання № 2 складається із трьох частин і перевіряє вміння знаходити радіус, область збіжності степеневого ряду, а також досліджувати поводження ряду в граничних точках інтервалу.
Для відповіді на завдання № 3 необхідно знати розкладання функцій у ряд Маклорена.
Завдання № 4 складається із двох частин. Для рішення цього завдання необхідно обчислювати значення функції з необхідним ступенем точності.
Завдання № 5 містить чотири частини й перевіряє вміння за допомогою розкладання в ряд обчислювати інтеграли із заданою точністю.
Завдання № 6 складається із чотирьох частин. Для рішення цього завдання необхідно вміти застосовувати розкладання в ряд Тейлора для рішення диференціальних рівнянь із заданими початковими умовами.
Завдання № 7 містить чотири частини й перевіряє вміння студентів розкладати задану функцію в ряд Фур'є.
Приклад тесту до АКР
Завдання № 1
Який з поданих функціональних рядів є степеневим?
а) 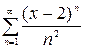 , б) , б)  , в) , в) 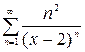 , г) , г)  . .
|
Завдання № 2
 Знайти області збіжності ряду Знайти області збіжності ряду 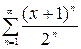 . .
|
2.1. Знайти центр інтервалу збіжності:
а) 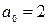 , б) , б) 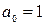 , в) , в) 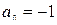 , г) , г) 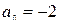 . .
|
2.2. Знайти радіус інтервалу збіжності:
а) 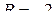 , б) , б)  , в) , в)  , г) , г) 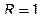 . .
|
2.3. Дослідити поводження ряду в граничних точках і знайти область збіжності:
а) 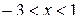 , б) , б) 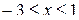 , в) , в) 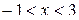 , г) , г) 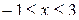 . .
|
Завдання № 3
 Знайти коефіцієнт при Знайти коефіцієнт при  в розкладанні функції в розкладанні функції 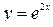 в ряд Маклорена.
а) в ряд Маклорена.
а)  , б) , б)  , в) , в) 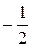 , г) , г) 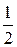 . .
|
Завдання № 4
Обчислити 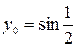 використовуючи два члени ряду та знайти
погрішність обчислювань використовуючи два члени ряду та знайти
погрішність обчислювань  . .
|
4.1. Функції  відповідає розкладання
а) відповідає розкладання
а) 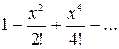 , б) , б) 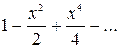 , в) , в) 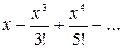 , г) , г)  . .
|
4.2. Вказати значення  та та  а)
а) 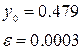 , б) , б)  , в) , в) 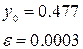 , г) , г) 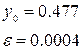 . .
|
Завдання № 5
 Обчислити Обчислити 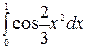 з точністю з точністю 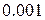
|
5.1. Функції 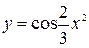 відповідає розкладання
а) відповідає розкладання
а) 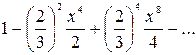 , б) , б)  ,
в) ,
в) 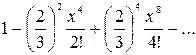 , г) , г) 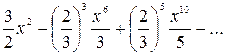 . .
|
5.2. Після інтегрування отримаємо ряд
а) 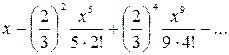 , б) , б) 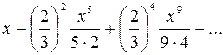 ,
в) ,
в) 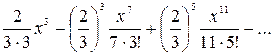 , г) , г) 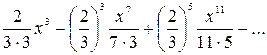 . .
|
| 5.3. Для обчислення з необхідним ступенем точності достатньо використати а) один член ряду, б) два члени ряду, в) три члени ряду, г) чотири члена ряду. |
5.4. Наближеним значенням 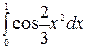 є
а) є
а)  , б) , б)  , в) , в) 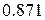 , г) , г) 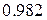 . .
|
Завдання № 6
 Знайти розкладання в степеневий ряд по ступенях Знайти розкладання в степеневий ряд по ступенях 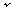 рішення диференційного рівняння рішення диференційного рівняння  , , 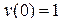 (члени розкладання, що відрізняються від нуля) (члени розкладання, що відрізняються від нуля)
|
6.1. Перший член розкладання має вигляд
а) 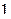 , б) , б)  , в) , в)  , г) , г) 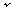 . .
|
6.2. Другий член розкладання має вигляд
а) 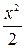 , б) , б)  , в) , в)  , г) , г) 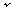 . .
|
6.3. Третій член розкладання має вигляд
а) 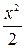 , б) , б)  , в) , в) 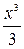 , г) , г)  . .
|
6.4. Розкладання в степеневий ряд рішення диференційного рівняння  , (три перших члени) мають вигляд
а) , (три перших члени) мають вигляд
а) 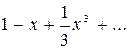 , б) , б)  ,
в) ,
в)  , г) , г) 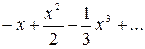 . .
|
Завдання № 7
7. Розкласти в ряд Фур’є функцію 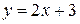 , що заданий на інтервалі , що заданий на інтервалі 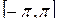
|
7.1. Визначити коефіцієнт  а)
а) 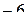 , б) , б) 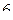 , в) , в) 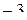 , г) , г)  . .
|
7.2. Визначити коефіцієнт 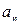 а)
а) 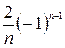 , б) , б) 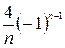 , в) , в)  , г) , г)  . .
|
7.3. Визначити коефіцієнт  а)
а) 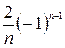 , б) , б) 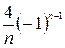 , в) , в)  , г) , г)  . .
|
7.4. Розкладання має вигляд
а) 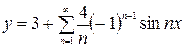 , б) , б) 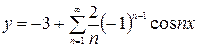 ,
в) ,
в)  ,
г) ,
г)  . .
|
ВИКОРИСТАНА ЛІТЕРАТУРА
1. Шнейдер В.Е., Слуцкий А.И., Шулов А.С. Краткий курс высшей математики. – М., Высшая школа, 1978, 670 с.
2. Гусак А.А. Задачи и упражнения по высшей математике. В 2 ч. Для вузов.-2-е изд., перераб.-Минск: Высш. шк.,1988.- Ч. 1., 247с.
3. Глаголев А.А., Солнцева Т.В. Курс высшей математики. М.: Высш. шк.,1965.- 591 с.
4. Сборник задач по курсу высшей математики/ Под редакцией Г.И.Кручковича, 3- е изд., перераб.- М.:Высшая школа,1973.- 576 с.
 2020-08-05
2020-08-05 117
117







