Завдання № 1 Обчислити приблизно з точністю до  .
.
1.1  1.2
1.2 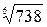
1.3  1.4
1.4 
1.5 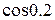 1.6
1.6 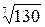
Завдання № 2 Обчислити приблизно інтеграл з точністю до  .
.
2.1 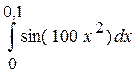 , 2.2
, 2.2  ,
,
2.3  , 2.4
, 2.4 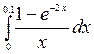 ,
,
2.5  , 2.6.
, 2.6. 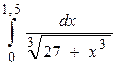
Завдання № 3
Знайти перші чотири члени розкладання в степеневої ряд рішення диференціального рівняння, що задовольняє початковим умовам.
3.1 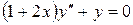 ,
, 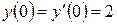 ,
,
3.2  ,
, 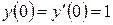 ,
,
3.3 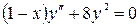 ,
, 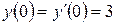 ,
,
3.4 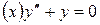 ,
, 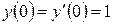 ,
,
3.5 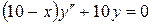 ,
,  ,
,
3.6 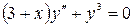 ,
,  .
.
Практичне заняття №4
Тема: Розкладання функцій у ряд Фур’є.
Література: [1,2].
Ціль: Розкладати різні функції в тригонометричні ряди Фур’є
План
Розкладання функцій у ряд Фур'є
Розкладання функцій у ряд Фур'є
Завдання № 1 Розкласти задану функцію в ряд Фур’є на проміжку 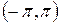 .
.
1.1. 
Рішення:
Визначимо коефіцієнти ряду
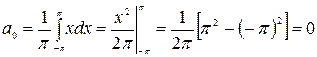 .
.
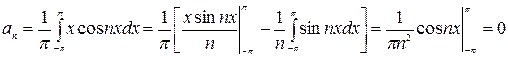

 .
.
Дійсно, нульовими є коефіцієнти при синусах.
Отже, шукане розкладання має вигляд

або
 .
.
1.2. 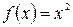
Рішення:
Рішення
Тому що функція 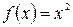 , то коефіцієнти
, то коефіцієнти 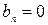 . Визначимо коефіцієнти
. Визначимо коефіцієнти 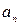
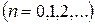 .
.
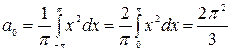 ;
;
 .
.
Виходить, ряд Фур'є даної функції має вигляд
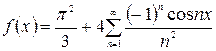 .
.
ЗАВДАННЯ ДЛЯ ПРАКТИЧНОГО ЗАНЯТТЯ № 4
Завдання № 1 Розкласти в ряд Фур’є.
1.1 
1.2 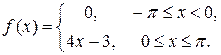
1.3 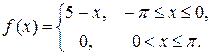
1.4 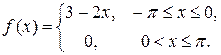
1.5 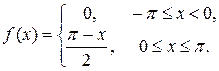
1.6 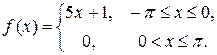
Домашня контрольна робота (ДКР)
Умови виконання
1. Для даденного функціонального ряду побудувати мажоруючий ряд і знайти інтервал рівномірної збіжності на зазначеному інтервалі.
2. Знайти область збіжності степеневого ряду.
3. Розвинути функцію в ряд Тейлора за ступенями  .
.
4. Застосовуючи розкладання функції в степеневий ряд, обчислити її значення з точністю до 0,001.
5. Обчислити інтеграл з точністю до 0,001.
6. Знайти три перших відмінних від нулі члена розкладання в степеневий ряд рішення диференціального рівняння, що задовольняє початковій умові.
7. Розкласти в ряд Фур’є періодичну (з періодом 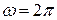 ) функцію
) функцію 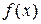 , що завдана на відрізку
, що завдана на відрізку 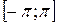 .
.
Варіанти завдань до ДКР
Варіант 1
1. 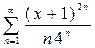 ,
, 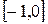 2.
2. 
3.  4.
4. 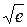
5. 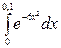 6.
6.  ,
, 
7. 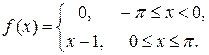
Варіант 2
1. 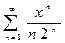 ,
, 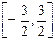 2.
2. 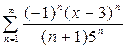
3. 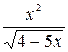 4.
4. 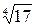
5. 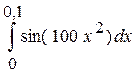 6.
6. 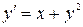 ,
, 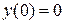
7. 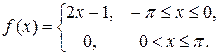
Варіант 3
1.  ,
, 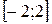 2.
2. 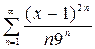
3. 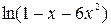 4.
4. 
5.  6.
6. 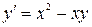 ,
, 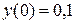
7. 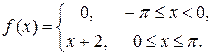
Варіант 4
1. 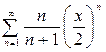 ,
, 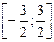 2.
2. 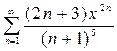
3. 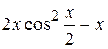 4.
4. 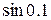
5.  6.
6.  ,
, 
7. 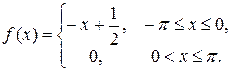
Варіант 5
1.  ,
, 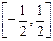 2.
2. 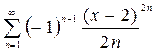
3. 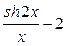 4.
4. 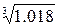
5. 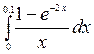 6.
6. 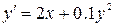 ,
, 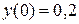
7. 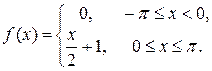
Варіант 6
1. 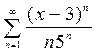 ,
, 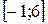 2.
2. 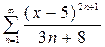
3. 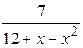 4.
4. 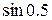
5. 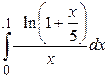 6.
6.  ,
, 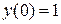
7. 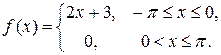
Варіант 7
1. 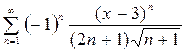 ,
,  2.
2. 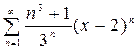
3. 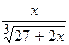 4.
4. 
5. 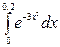 6.
6. 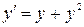 ,
, 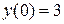
7. 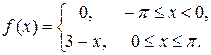
Варіант 8
1. 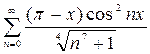 ,
, 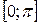 2.
2. 
3. 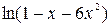 4.
4. 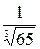
5. 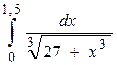 6.
6. 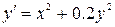 ,
, 
7. 
Варіант 9
1.  ,
,  2.
2. 
3. 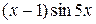 4.
4. 
5. 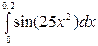 6.
6.  ,
, 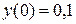
7. 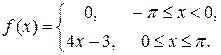
Варіант 10
1. 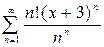 ,
,  2.
2. 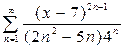
3.  4.
4. 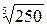
5. 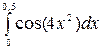 6.
6.  ,
, 
7. 
Варіант 11
1. 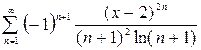 ,
,  2.
2. 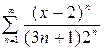
3.  4.
4. 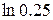
5.  6.
6. 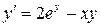 ,
, 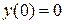
7. 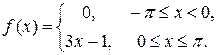
Варіант 12
1. 1. 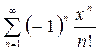 ,
, 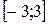 2.
2. 
3. 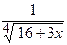 4.
4. 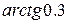
5.  6.
6.  ,
, 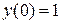
7. 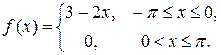
Варіант 13
1. 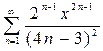 ,
,  . 2.
. 2. 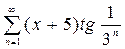
3. 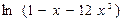 4.
4. 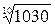
5.  6.
6.  ,
, 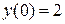 .
.
7. 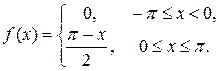
Варіант 14
1. 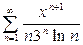 ,
,  . 2.
. 2. 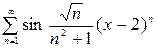
3.  4.
4. 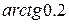
5. 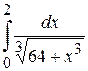 6.
6.  ,
, 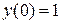 .
.
7. 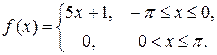
Варіант 15
1. 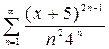 ,
,  2.
2. 
3. 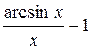 4.
4. 
5.  6.
6. 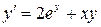 ,
, 
7. 
Варіант 16
1.  ,
, 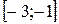 2.
2. 
3. 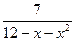 4.
4. 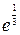
5.  6.
6. 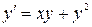 ,
, 
7. 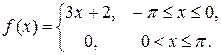
Варіант 17
1. 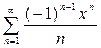 ,
, 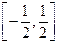 2.
2. 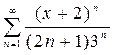
3. 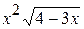 4.
4. 
5.  6.
6.  ,
, 
7. 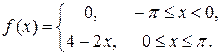
Варіант 18
1.  ,
,  2.
2. 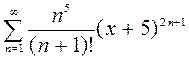
3.  4.
4. 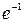
5. 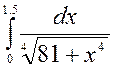 6.
6. 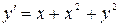 ,
, 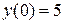 .
.
7. 
Варіант 19
1. 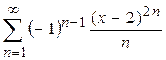 ,
, 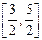 2.
2. 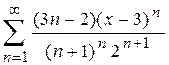
3.  4.
4. 
5. 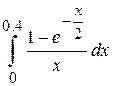 6.
6.  ,
, 
7. 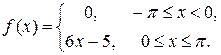
Варіант 20
1.  ,
, 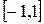 2.
2. 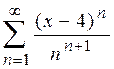
3.  4.
4. 
5.  6.
6. 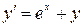 ,
, 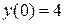
7. 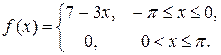
Варіант 21
1. 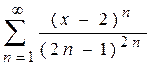 ,
,  2.
2. 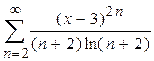
3. 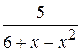 4.
4. 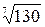
5.  6.
6. 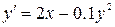 ,
, 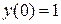
7. 
Варіант 22
1. 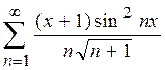 ,
, 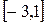 2.
2. 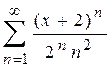
3.  4.
4. 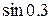
5. 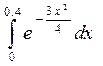 6.
6. 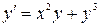 ,
, 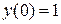 .
.
7. 
Варіант 23
1. 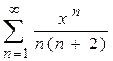 ,
, 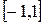 2.
2. 
3. 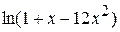 4.
4. 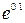
5.  6.
6. 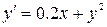 ,
, 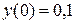 .
.
7. 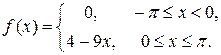
Варіант 24
1.  ,
, 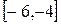 2.
2. 
3. 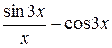 4.
4. 
5. 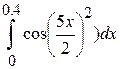 6.
6. 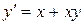 ,
, 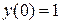
7. 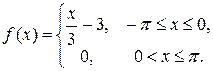
Варіант 25
1. 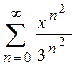 ,
, 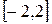 . 2.
. 2. 
3. 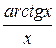 4.
4. 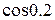
5.  6.
6. 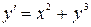 ,
, 
7. 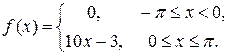
Варіант 26
1. 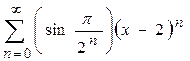 ,
,  2.
2. 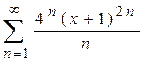
3. 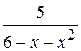 4.
4. 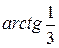
5.  6.
6. 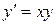 ,
, 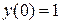
7. 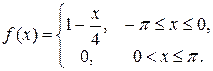
Варіант 27
1. 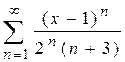 ,
, 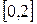 2.
2. 
3.  4.
4. 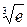
5.  6.
6. 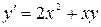 ,
, 
7. 
Варіант 28
1.  ,
,  2.
2. 
3. 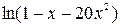 4.
4. 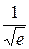
5. 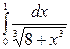 6.
6.  ,
, 
7. 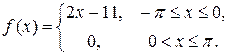
Варіант 29
1. 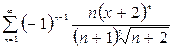 ,
, 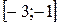 2.
2. 
3. 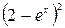 4.
4. 
5. 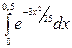 6.
6. 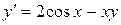 ,
, 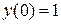
7. 
Варіант 30
1.  ,
, 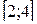 2.
2. 
3.  4.
4. 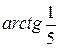
5.  6.
6. 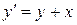 ,
, 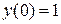
7. 
Теоретичні питання
1. Який ряд називається степеневим.
2. Радіус збіжності степеневого ряду.
3. Область збіжності степеневого ряду.
4. Ряд Тейлора й Маклорена.
5. Розкладання в степеневі ряди елементарних функцій.
6. Застосування рядів Тейлора й Маклорена.
7. Розкладання в ряд Фур'є парних функцій.
8. Розкладання в ряд Фур'є непарних функцій.
9. Розкладання в ряд Фур'є функцій загального виду.
 2020-08-05
2020-08-05 108
108








