Завдання для практичного заняття № 1

 

 Завдання № 1 Досліджувати на збіжність степеневої ряд

1.1 ,               1.2 ,                                                                       

1.3 ,               1.4 ,                                                                       

1.5 ,               1.6 ,                                                                       

1.7 ,               1.8.                                                               

                                                       

                                                       

Практичне заняття №2

 

Тема: Розкладання функцій у степеневі ряди.

Література: [1.2].

Ціль: Навчитися використовуючи відомі розкладання, розкладати в степеневі ряди різні функції.

 

План

1.Розкладання функцій у степеневі ряди.

 

Розкладання функцій у степеневі ряди.

Завдання № 1

Розкласти в ряд Маклорена функцію

                                                                              

 

Рішення:

Скориставшись розкладанням синуса в ряд Маклорена, кожний член ряду розділимо на . Тоді

Очевидно, що розкладання справедливо для .

 

 

ЗАВДАННЯ ДЛЯ ПРАКТИЧНОГО ЗАНЯТТЯ № 2

 

 Завдання № 1 Розкласти в ряд Маклорена функцію

1.1 ,                            1.2 ,

1.3 ,                              1.4 ,

1.5 ,                                      1.6

 

                                                       

Практичне заняття №3

 

Тема: Застосування степеневих рядів.

Література: [1.2].

Ціль: Навчитися за допомогою розкладання в степеневі ряди різні ряди обчислювати із заданим ступенем точності значення функцій, визначених інтегралів, а також вирішувати диференціальні рівняння.

 

План

1. Наближене обчислення значень функцій.

2. Наближене обчислення інтегралів.

3. Наближене рішення диференціальних рівнянь.

 

Наближене обчислення значень функцій.

Завдання № 1

  Обчислити  з точністю до .

 

Рішення:

Очевидно, що .

Підставляючи ,  у розкладання в ряд, одержимо

 

 

 

Отриманий ряд є знакопереможним рядом, що задовольняють умовам ознаки Лейбниця. Оскільки погрішність при заміні такого ряду сумою його перших членів не перевищує модуля першого відкинутого члена й , те для того, щоб одержати шукане значення із заданою точністю, досить взяти суму перших трьох членів. Тоді

.

Отже,

.

 

Завдання № 2

Обчислити  з точністю до .

Рішення:

Даний інтеграл є що не береться, тобто не виражається кінцевою комбінацією елементарних функцій. Застосуємо розкладання в ряд. Тоді

 

 

Оскільки отриманий знакопереможний ряд задовольняє умовам ознаки Лейбниця й , те, взявши перші його два члени, одержимо .

 

 

Завдання № 3

Знайти перші чотири члени розкладання в степеневої ряд рішення диференціального рівняння , що задовольняє початковим умовам .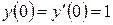

 

Рішення:

Запишемо ряд Маклорена у вигляді

Перші два члени розкладання є початковими умовами , . З диференціального рівняння треба:

, значить .

Продиференціюємо вихідне рівняння. Тоді

.

Виражаючи , одержуємо , а значить .

Підставляючи значення функції і її похідних у розкладання , маємо