Область збіжності степеневого ряду

Степеневі ряди

 

Велике практичне

 значення мають ряди виду 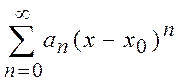, що називаються степеневими рядами. При  степеневий ряд має найпростіший вигляд .

    Областю збіжності будь-якого степеневого ряду є інтервал на числовій прямій довжиною 2R з центром у точці 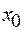 . Число R називається радіусом збіжності степеневого ряду.

 

Інтервал збіжності степеневого ряду можна знаходити безпосередньо, використовуючи, наприклад, ознаки Д’аламбера або Коші, втім часто зручніше користуватись формулами обчислення радіусу збіжності.

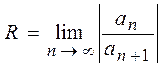, або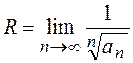

 

Зазначені формули містять не члени 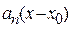 степеневого ряду, а лише коефіцієнти  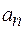цього ряду.

Розкладання функцій у ряди Тейлора й Маклорена

Важливим інструментом математичного аналізу є розвинення функцій у степеневі ряди.

Нехай задана функція 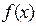. Степеневий ряд

називається рядом Тейлора цієї функції в околі точк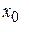и . При 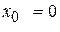 ряд Тейлора називається рядом Маклорена. Процес розвинення функцій у ряд Тейлора спрощується при використанні стандартних формул розвинення елементарних функцій. Наведемо основні з них.

;

;

;

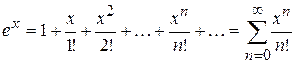(біноміальний ряд). Зокрема, при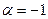

;

;

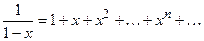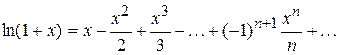і, як наслідок

 .

    Зауважимо, що якщо перші чотири ряди збігаються на всій числовій прямій, останні чотири ряди мають зміст лише при .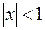

    Також часто застосовуються розкладання розвинення:

;

;

, .

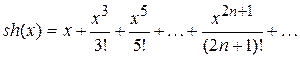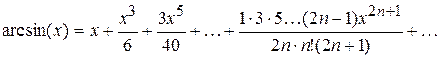    Відзначимо, що розкладання в ряд має важливе практичне застосування. Так за допомогою рядів можна із заданої степеню точності знаходити значення функцій, обчислювати інтеграли й визначати рішення диференціальних рівнянь.

 

 

Розкладання функцій у ряд Фур'є

 

 

На проміжку 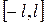 розкладання в ряд Фур'є заданої функції має вигляд

,

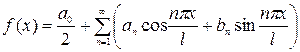де

, , ,

 

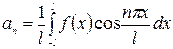ПРАКТИЧНА ЧАСТИНА

Практичне заняття №1

 

Тема: Область збіжності степеневого ряду.

Література: [1.2].

Ціль: Навчитися знаходити радіус і область збіжності степеневого ряду; уміти досліджувати поводження ряду в граничних точках інтервалу збіжності.

 

План

1.Область збіжності степеневого ряду.

 

Область збіжності степеневого ряду.

Завдання № 1 Досліджувати на збіжність степеневої ряд

1.1.                                                                                       

 

Рішення:

Розглянемо ряд, що складається з модулів членів ряду. Застосовуючи ознаку Д’аламбера, маємо

.

 

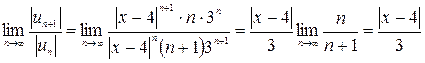Ряд сходиться, якщо 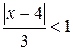. Розкриваючи модуль, одержуємо

.

Тобто даний ряд сходиться при 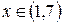 із центром у точці 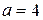, і розходиться при .

Досліджуємо збіжність ряду на кінцях області збіжності, тобто в точках , .

При  одержуємо розбіжний ряд Дирихле .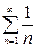

Якщо 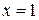, одержуємо знакопереможний ряд .

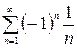Тому що цей ряд задовольняє умовам ознаки Лейбниця, він сходиться умовно.

Отже, досліджуваний ряд сходиться для .

 

1.2.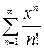

 

Рішення:

Розглянемо ряд, складений з модулів членів ряду.

По ознаці Д’аламбера

.

Тобто досліджуваний ряд сходиться на всій числовій осі при .