Цель работы: изучить движение заряженных частиц в магнитном поле; ознакомиться с методом магнетрона; определить удельный заряд электрона методом магнетрона.
ВВЕДЕНИЕ
На заряженную частицу q, движущуюся со скоростью 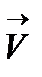 в магнитном поле, индукция которого равна
в магнитном поле, индукция которого равна 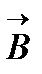 , действует сила
, действует сила 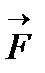 . Эта сила называется силой Лоренца, или магнитной силой, и выражается формулой:
. Эта сила называется силой Лоренца, или магнитной силой, и выражается формулой:
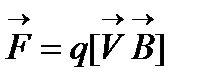 . (1)
. (1)
Сила Лоренца направлена перпендикулярно плоскости, в которой лежат векторы 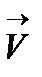 и
и 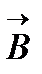 , её направление определяется правилом левой руки. Модуль силы Лоренца выражается формулой:
, её направление определяется правилом левой руки. Модуль силы Лоренца выражается формулой:
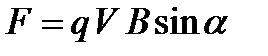 , (2)
, (2)
где a - угол между векторами 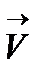 и
и 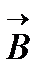 .
.
Траектория заряженной частицы в магнитном поле зависит от конфигурации поля, ориентации и величины вектора 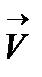 , отношения заряда частицы к её массе. Это отношение называется удельным зарядом частицы.
, отношения заряда частицы к её массе. Это отношение называется удельным зарядом частицы.
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
В работе используются следующие приборы и оборудование:
ФПЭ-03 – кассета (включает в себя катушку индуктивности, внутри которой находится электронный вакуумный диод); ИП – источник питания; микроамперметр.
Сущность метода магнетрона, используемого в работе, состоит в следующем: электронный вакуумный диод, электроды которого представляют собой коаксиальные цилиндры, помещается внутри катушки так, что ось лампы (катод) совпадает с осью катушки (осью Z).
Когда лампа включена в электрическую цепь, электроны, вылетающие из катода (К) лампы, при отсутствии тока в катушке движутся радиально к аноду (А). При пропускании тока через катушку лампа окажется в магнитном поле, параллельном оси лампы. На электроны, движущиеся от катода к аноду, начинает действовать сила Лоренца, вследствие чего траектория электрона начнет искривляться.
При определенном отношении между скоростью электрона и индукцией магнитного поля катушки электроны перестанут достигать анода, т.е. ток в лампе прекратится.
Рассмотрим движение электрона в лампе при наличии магнитного поля. Воспользуемся цилиндрической системой координат (см. рис. 1), тогда положение электрона определяется его расстоянием r от оси и полярным углом 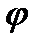 .
.
Электрон, вылетающий из катода, движется в плоскости, перпендикулярной оси Z, совпадающей с направлением магнитного поля катушки с током. (Ось Z перпендикулярна к плоскости чертежа, см. рис. 1).
| r |
| К |
| j |
 |
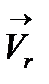 |
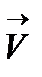 |
| Z |
| A |
Рис. 1.
Момент импульса электрона 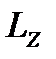 относительно оси Z равен:
относительно оси Z равен:
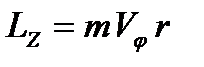 , (3)
, (3)
где 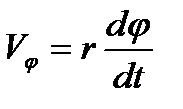 - составляющая скорости, перпендикулярная радиусу r, m – масса электрона.
- составляющая скорости, перпендикулярная радиусу r, m – масса электрона.
Момент магнитной силы 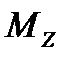 , действующий на электрон, будет равен:
, действующий на электрон, будет равен:
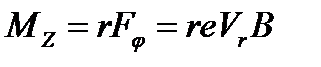 , (4)
, (4)
где 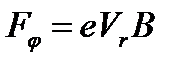 ,
, 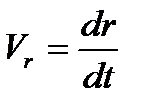 - радиальная составляющая скорости электрона, е – заряд электрона. Запишем основное уравнение динамики вращательного движения:
- радиальная составляющая скорости электрона, е – заряд электрона. Запишем основное уравнение динамики вращательного движения:
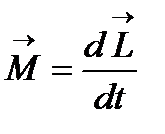 . (5)
. (5)
Спроецируем (5) на ось Z и подставим 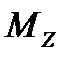 и
и 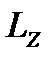 , тогда имеем:
, тогда имеем:
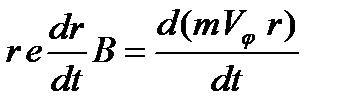 . (6)
. (6)
Проинтегрировав уравнение (6), получим:
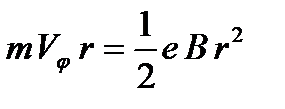 . (7)
. (7)
Из (7) найдем 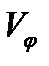 :
:
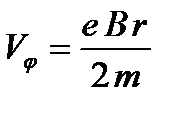 . (8)
. (8)
Кинетическая энергия электрона равна работе сил электрического поля по его перемещению:
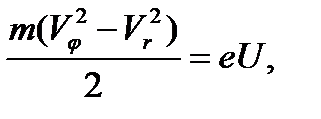 (9)
(9)
где U – потенциал относительно катода точки поля, в которой находится электрон.
Подставляя в (9) значение 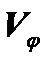 из (8), получим:
из (8), получим:
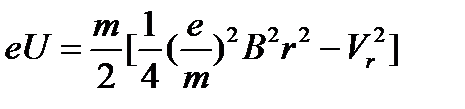 . (10)
. (10)
При некотором критическом значении индукции магнитного поля В кр, скорость электрона вблизи анода станет перпендикулярной к радиусу r, т.е. 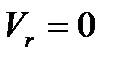 . Тогда уравнение (10) примет вид:
. Тогда уравнение (10) примет вид:
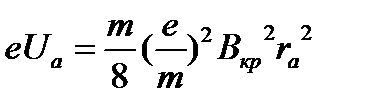 , (11)
, (11)
где U а – потенциал анода относительно катода (анодное напряжение) при критическом токе Ikp, rа – радиус цилиндрического анода лампы.
Из (11) находим выражение для удельного заряда электрона:
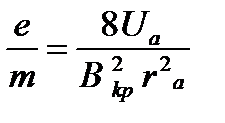 . (12)
. (12)
Критическое значение магнитной индукции катушки с током Ikp определяется из формулы:
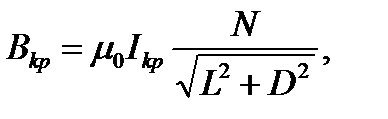 (13)
(13)
где m0 = 4p×10-7 Гн/м – магнитная постоянная, N = 2500 – число витков катушки, L = 168 мм – длина катушки, D = 85 мм – диаметр катушки. Радиус анода лампы: ra = 1,7 мм.
Таким образом, удельный заряд электрона можно вычислить, экспериментально определив Вкр, для чего необходимо найти критическое значение тока Ikp.
| mA |
| V |
| A |
| RC |
| R |
| ° ° 24 B |
| °6, 3 B ° |
| ° ° |
| ИП |
| ФПЭ-03 |
Рис. 2.
1. Включить установку (рис. 2). Дать прогреться лампе в течение 5 мин. Установить значение тока IК = 0,4 А и напряжение UА = 40 B.
2. Изменяя ток, текущий через катушку IК в пределах от 0,4 до 2,4 А через 0,2 А, произвести измерения анодного тока IА миллиамперметром mА.
Таблица 1
| IК, A | UА = 40 B |
| IА, mA | |
| 0,4 | |
| 0,6 | |
| 0,8 | |
| 1,0 | |
| 1,2 | |
| 1,4 | |
| 1,6 | |
| 1,8 | |
| 2,0 | |
| 2,2 | |
| 2,4 |
Значения IК и IА занести в таблицу 1.
3. По результатам измерений IК и IА построить график IА = j (Iк), который называется сбросовой характеристикой (см. рис. 3).
| IA |
| 0 |
| Iкр |
| IК |
Рис. 3.
4. Найти критическое значение тока Iкр в катушке, для чего провести до взаимного пересечения касательную к точке перегиба сбросовой характеристики (на участке её спада) и прямую линию, соответствующую изменению минимальных значений анодного тока (как показано на рис. 3). Занести значение Iкр в таблицу 2.
5. Определить критическое значение Bkp индукции магнитного поля по формуле (13) и занести его в таблицу 2.
Таблица 2
| UА, В | Iкр, мА | Bkp, Тл | (e/m)экс, Кл/кг | (e/m)табл, Кл/кг | e |
| 40 |
6. Вычислить удельный заряд электрона по формуле (12).
7. Вычислить относительную погрешность e полученной величины e/m по формуле:
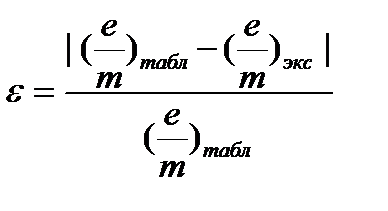 . (14)
. (14)
Результаты расчетов записать в таблицу 2.
КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ СДАЧИ РАБОТЫ
1. Что называется удельным зарядом? Каковы единицы его измерения?
2. В чем суть метода магнетрона для определения удельного заряда электрона?
3. Записать выражение для силы Лоренца в векторном и скалярном видах.
4. Какой вид будет иметь траектория заряженной частицы, если она движется в однородном магнитном поле со скоростью 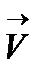 , перпендикулярной вектору
, перпендикулярной вектору 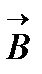 ?
?
 2020-08-05
2020-08-05 901
901








