Уравнения Максвелла и их физический смысл

· Физика

Уравнения Максвелла у многих вызывают какой-то полумистический трепет, основанный на убеждении, что понять их очень трудно, что для этого нужна солидная математическая подготовка. В то же время они достаточно просты и смысл их при внимательном чтении приведенного ниже материала вполне понятен для учеников старших классов средней школы. Вспомним, как возникает магнитное поле вокруг проводников с током: силовые линии имеют вид колец, "надетых" на вектор, показывающий направление тока. Первое уравнение Максвелла об этом и говорит: rotH=j_пр + dD/dt.

Математическая операция rotH (rot-ротор, или вихрь) означает: на направление (вектор) тока "надевается" маленькое воображаемое колечко (рис. 9,а). Значение касательной к колечку, т. е. составляющей напряженности магнитного поля Н, умножается на длину окружности (колечка) и делится на площадь этого колечка. Ротор Н отличен от нуля только для вихревого поля с кольцеобразными замкнутыми силовыми линиями. Показанный на рисунке вектор j_пpобозначает плотность протекающих сквозь колечко реальныхтоков проводимости, т. е. токов, которые протекают в токопроводящей среде (например в металле):
j_пр = 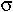E
где 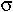- проводимость среды, Е - напряженность электрического поля.

Но магнитное поле Н создается не только токами проводимости, но и изменениями вектора электрической индукции D. Это изменение D отражено в формуле rot H=dD/dt, что означает: очень малая часть вектора D (обозначено dD) изменяется в очень малое время dt. Вектор в любой среде связан с напряженностью электрического поля:

D = 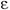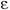₀E.

Производную по времени D (которая может быть обозначена как dD/dt) Максвелл назвал током смещения j_см. Он при этом имел ввиду, что под действием колебаний электрического поля заряды, находящиеся в среде, смещаются от своего положения равновесия. Таким образом, вектор тока, как и показано на рис. 9,а, состоит из двух составляющих: j_пр+j_см.

Здесь уместно сказать, что первое уравнение дает прекрасный критерий для различения диэлектриков и проводников. Если в среде токи проводимости больше токов смещения, то среда - проводник, если меньше, то диэлектрик. Идеальный диэлектрик - вакуум, в котором токи проводимости вообще отсутствуют. Колебания тока проводимости синфазны с колебаниями электрического поля, поэтому токи проводимости вызывают выделение энергии в среде с проводимостью, что приводит к тепловым потерям и уменьшению энергии электромагнитного поля.

Реальные среды всегда имеют некоторые потери. Они характеризуются углом потерь, определяемым по графику рис. 9,б, где по горизонтальной оси откладывается значение токов смещения, а по вертикальной - проводимости. Если предположить, что электрическое поле меняется по синусоидальному закону с угловой частотой 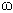, то амплитуда токов смещения будет пропорциональна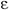 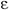₀ .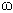

Из этого выражения может быть сделан важный вывод: свойства сред зависят от частоты, и вещество, по своим свойствам близкое к проводнику на низких частотах, может проявлять свойства диэлектрика на высоких.

Итак, первое уравнение Максвелла утверждает, что изменения электрического поля порождают вихревое магнитное поле.

Второе уравнен ие Максвелла выражает закон электромагнитной индукции Фарадея: ЭДС в любом замкнутом контуре равна скорости изменения (т. е. производной по времени) магнитного потока. Но ЭДС равна касательной составляющей вектора напряженности электрического поля Е, помноженной на длину контура. Чтобы перейти к ротору, как и в первом уравнении Максвелла, достаточно разделить ЭДС на площадь контура, а последнюю устремить к нулю, т. е. взять маленький контур, охватывающий рассматриваемую точку пространства (рис. 9,в). Тогда в правой части уравнения будет уже не поток, а магнитная индукция, поскольку поток равен индукции, помноженной на площадь контура.

Итак, получаем: rotE = - dB/dt.

Таким образом, вихревое электрическое поле порождается изменениями магнитного, что и подано на рис. 9,в и представлено только что приведенной формулой.

Третье и четвертое уравнения Максвелла имеют дело с зарядами и порождаемыми ими полями. Они основаны на теореме Гаусса, утверждающей, что поток вектора электрической индукции через любую замкнутую поверхность равен заряду внутри этой поверхности.

Немного поясним, что такое поток. Если скорость истечения воды из водопроводного крана помножить на площадь отверстия крана, мы получим поток воды - ее расход в кубометрах за секунду (рис. 9,г). Если магнитную индукцию электромагнита помножить на площадь сечения его магнитопровода, получится магнитный поток, определяющий силу притяжения.

В теореме Гаусса для определения потока электрической индукции проще всего взять сферическую поверхность (рис. 9,д) площадью S, во всех точках которой вектор D имеет одинаковое абсолютное значение. По теореме Гаусса SD = q, где q - заряд, помещенный внутри поверхности. Если это точечный заряд, помещенный в центре сферы, то мы получаем простые формулы:

- для определения его электрической индукции

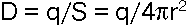
- для определения напряженности электрического поля

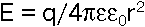
Вернемся к рис. 9,д. Если поток вектора D через замкнутую поверхность S разделить на объем, заключенный внутри поверхности, и мысленно стянуть поверхность в точку, получим так называемую в математике дивергенцию (или извержение) вектора. В правой части уравнения для потока стоит заряд q. Деленный на объем, он дает объемную плотность заряда г. Итак, получено третье уравнение Максвелла:

div D = р.

Четвертое уравнение утверждает, что магнитных зарядов в природе не существует, поэтому

div B = 0.

На уравнениях Максвелла основана целая наука - электродинамика, позволяющая строгими математическими методами решить множество полезных практических задач. Можно рассчитать, например, поле излучения различных антенн как в свободном пространстве, так и вблизи поверхности Земли или около корпуса какого-либо летательного аппарата, например, самолета или ракеты. Электродинамика позволяет рассчитать конструкцию волноводов и объемных резонаторов - устройств, применяющихся на очень высоких частотах сантиметрового и миллиметрового диапазонов волн, где обычные линии передачи и колебательные контуры уже непригодны. Без электродинамики невозможно было бы развитие радиолокации, космической радиосвязи, антенной техники и многих других разделов современной радиотехники.

Сами по себе уравнения Максвелла допускают множество различных решений. Чтобы их конкретизировать, задают начальные и граничные условия. Начальные условия - это распределение в пространстве и во времени токов и зарядов, создающих поля. Граничные условия относятся к окружающему пространству - сюда может входить и поверхность Земли с ее известными параметрами, металлические стенки волноводов и т. д. Одно из граничныхусловий, например, утверждает, что вблизи хорошо проводящей поверхности не может существовать касательная составляющая электрического поля - силовые линии должны входить в поверхность перпендикулярно ей. Не всегда удается получить решения уравнении аналитически, и тогда неоценимую помощь оказывают компьютеры, позволяя решить уравнения численными методами.